考研数学二（线性代数）模拟试卷103

考研数学二（线性代数）模拟试卷103

选择题

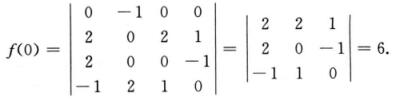
1.多项式(C)

A. 2

B. 4

C. 6

D. 8

解析：要求多项式的常数项，只需令x=0求行列式的值即可，故

2.设3阶矩阵A与B等价，则下列结论正确的是（ ）．(D)

A. 存在可逆矩阵P，使得PA=B

B. 存在可逆矩阵Q，使得AQ=B

C. 若r(A)=2，A可经初等行变换化为矩阵B

D. 若r(A)=3，A可经初等列变换化为矩阵B

解析：当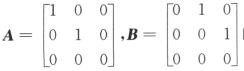时，矩阵A不能经初等行变换化为矩阵B，也不存在可逆矩阵P，使得PA=B，从而选项(A)，(C)不正确．

当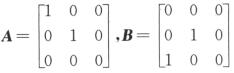

3.已知向量组α，β，γ线性无关，则k≠1是向量组α+kβ，β+kγ，α-γ线性无关的（ ）．(C)

A. 充分必要条件

B. 充分条件，但非必要条件

C. 必要条件，但非充分条件

D. 既非充分条件也非必要条件

解析：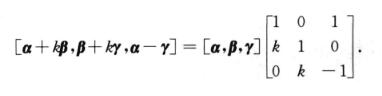

设

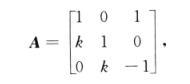
4.设A=[α₁，α₂，α₃]，α₁，α₂，α₃为线性无关的3维列向量，P为3阶矩阵，且PA=[-α₁，-2α₂，-3α₃]，则| P—E |=（ ）．(D)

A. 6

B. -6

C. 24

D. -24

解析：由题设，PA=P[α₁，α₂，α₃]=[α₁，α₂，α₃]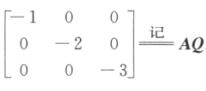

5.设A，B均为n阶矩阵，记r(X)为矩阵X的秩，[X，Y]表示分块矩阵，则（ ）．(A)

A. r([ A AB ])=r(A)

B. r([A BA])=r(A)

C. r([A B])=max{r(A)，r(B)}

D. r([A B])=r([A^T B^T])

解析：方法一 一方面，A是[A AB]的子矩阵，因此r([A AB])≥r(A)．

另一方面，[A AB]是A与[E B]的乘积，即[A AB]=A[E B]，因此r([A AB])≤r(A)，故r([A AB])=r(A)，选(A)．

方法二 设C=AB，则C的列向量可由A的列向量线性表示，故r([A AB])=r([A C])=r(A)，选(A)．

{注}①在方法一中，[A AB]=A[E B]，但是[A BA]≠[E B]A，因为不满足乘法规则．

②对于选项(B)，(C)(D)可举出反例。

取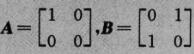，则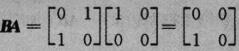，从而r(A)=1，r([A BA])=有r(A)≠r([A BA])，知选项(B)错误;

取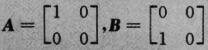，则r(A)=r(B)=1，而

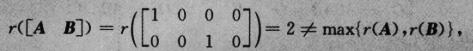
知选项(C)错误；

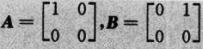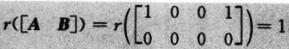取，则，而

r([A^T B^T])=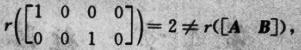

知选项(D)错误．

③若A_m×nB_n×s=O，将B，O按列分块，有

AB=A[β₁，β₂，…，β_s]=[Aβ₁，Aβ₂，…，Aβ_s]=[0，0，…，0].则Aβ_i<

本文档预览：3000字符，共15731字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载