考研数学二（高等数学）模拟试卷150

考研数学二（高等数学）模拟试卷150

选择题

1.当x→0时，以下无穷小中，阶数最高的是（ ）．

D

解析：当x→0时，

对于(A)选项，sin x～x，(1+x)^2/x→e²，则有

∫₀^sinx (1+t)^2/tdt～∫₀^x e²dt=e²x；

对于(B)选项，ln(1+x²)～x²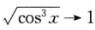，，则有

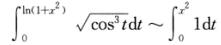=x²；

对于(C)选项，e^{cos x}-e^{sin x}→e-1，则有

∫₀^x(e^{cos t}-e^{sin t})dt～∫₀^x(e-1)dt=(e-1)x；

对于(D)选项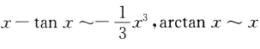，，则有

∫₀^{x-tan x}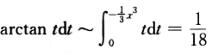

2.已知x=0是函数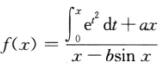(A)

A. (1，1)

B. (-1，1)

C. (1，-1)

D. (-1，-1)

解析：因为x=0是函数f(x)的第一类间断点，且f(x)在x=0处无定义，故f(x)的左、右极限均存在．又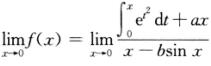为“0/0”型，故由洛必达法则得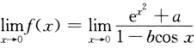

3.设函数f(x)在(-∞，+∞)内连续，其一阶导函数f’(x)的图形如图所示，并设在f’(x)存在处f\\(B)

A. 1

B. 2

C. 3

D. 4

解析：拐点与二阶导数有关，而题中给出的是f’(x)的图形，所以要由f’(x)推出f”(x)的大致图形，以此分析曲线y=f(x)的拐点个数．为叙述方便，重新画图并注以字母，如图所示．

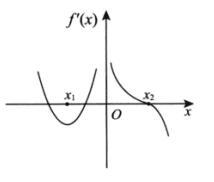
4.设函数f(x)在区间[0，1]上连续，在区间(0，1)内可导，且f’(x)＞0，f(0)=1，则当x∈(0，1)时，有（ ）．(A)

A. f(x)＜e^f(x)-1

B. f(x)＞e^f(x)-1

C. f(x)＜e^-f(x)+1

D. f(x)＞e^f(x)+1

解析：因为函数f(x)在区间[0，1]上连续，在区间(0，1)内可导，且f’(x)＞0，所以f(x)在[0，1]上单调增加，又f(0)=1，故当x∈(0，1)时，f(x)＞f(0)=1．

令F(x)=e^-f(x)f(x)，则F’(x)=e^-f(x)f’(x)[1-f(x)]＜0(0＜x＜1)．所以F(x)在[0，1]上单调减少，从而当x∈(0，1)时，有F(x)＜F(0)，即e^-f(x)f(x)＜e^-1，也即f(x)＜e^f(x)-1．

5.设I₁=∫₁^x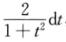，I₂=∫₁^x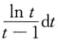,I₃=∫₁^x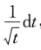(A)

A. I₁＜I₂＜I₃

B. I₁＜I₃＜I₂

C. I₂＜I₃＜I₁

D. I₃＜I₁＜I₂

解析：设f(t)=(1+t²)ln t-2(t-1)，则

因为当t＞1时，有本文档预览：3000字符，共13359字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载