考研数学二（高等数学）模拟试卷157

考研数学二（高等数学）模拟试卷157

选择题

1.设函数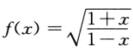(B)

A. a=1，b=1，c=1

B. a=1，b=1,c=1/2

C. a=0，b=-1，c=1/2

D. a=0，b=-1，c=1

解析：由在x=0处，满足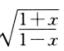=a+bx+cx²+…，知(a+bx+cx²+…)．

由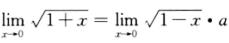，可得a=1．又

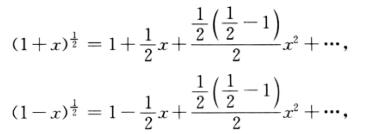
故

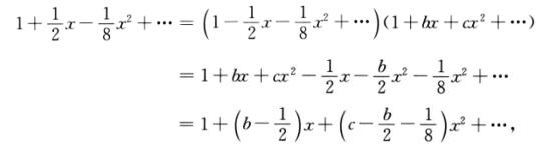
2.设f(x)在x=a的某邻域内有定义，在x=a的某去心邻域内可导，下述论断正确的是（ ）．

C

解析：C的证明．用反证法，设f’(a)存在，则f(x)在x=a处连续，再由题设，f(x)在x=a的某邻域内连续，从而

3.设函数f(x)在x=0的某邻域内有定义，则以下结论正确的是（ ）.(D)

A. 若f(0)=0，f’(0)=0，则x=0必不是极值点

B. 若f’(0)=0，f\\

C. 若f(0)=0，f’(0)＞0，则存在δ＞0，使得f(x)在(0，δ)内单调递增

D. 若f’(0)=0，f\\

解析：D项，由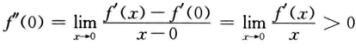

4.曲线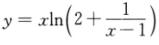的斜渐近线方程为（ ）．

B

解析：

故曲线的斜渐近线方程为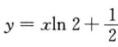

5.若方程ln x=kx有两个实根，则常数k的取值范围为（ ）．(B)

A. 0＜k＜1

B. 0＜k＜1/e

C. 1＜k＜e

D. 1/e＜k＜e

解析：令f(x)=ln x-kx，x ∈(0，+∞)，则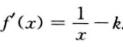显然，当k≤0时，f’(x)＞0，f(x)单调增加，方程f(x)=0不可能有两个实根．当k＞0时，f(x)有唯一驻点x=1/k．由于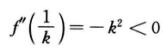，因此f(1/k)=-ln k-1为f(x)在(0，+∞)上的极大值．又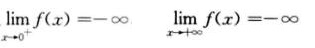

6.设三阶常系数齐次线性微分方程有特解cos x与e^2x，则该微分方程为（ ）．(B)

A. y’\\

B. y’\\

C. y’\\

D. y\\

解析：由一个特解为cos x，知特征方程有共轭复根±i，其特征方程含因式r²+1；由一个特解为e^2x，知特征方程有单实根2，其特征方程含因式r-2，则特征方程为(r²+1)(r-2)=0，整理得r³-2r²+r-2=0，故该三阶常系数齐次线性微分方程为y’\\

填空题

7.设f(ln x)=xln x，则fⁿ(x)=________．

e^x(x+n-1)

解析：由f’(lnx)=xlnx，则f’(x)=xe^x．由莱布尼茨公式，有

f⁽ⁿ⁾(x)=(xe^x)^(n-1)=e^xx+C_n-1¹e^x(x)’+0

=e^x(x+n-1)．

8.设函数y=y(x)由参数方程本文档预览：3000字符，共9748字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载