考研数学二（高等数学）模拟试卷154

考研数学二（高等数学）模拟试卷154

选择题

1.当x→0时，x-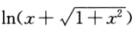(A)

A. 1/6，3

B. 1/6，2

C. 1/3，2

D. 1/3，3

解析：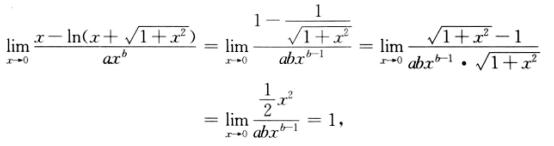

2.设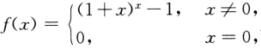(D)

A. 连续，但f’(0)不存在

B. f’(0)存在，但f’(x)在x=0处不连续．

C. f’(x)在x=0处连续，但f\\

D. f\\

解析：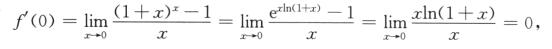

选项(A)错误．

当x≠0时，

f’(x)=[e^xln(1+x)-1]’=e^xln(1+x)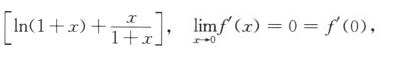

选项(B)错误．

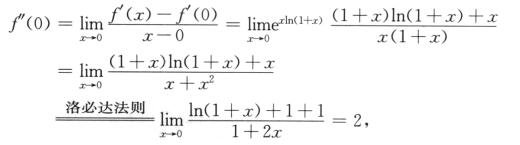
3.设函数f(x)在区间[-2，2]上可导，且f’(x)＞2f(x)＞0，则（ ）．

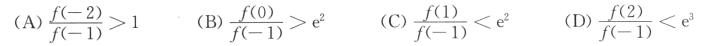
B

解析：令g(x)=e^-2xf(x)，则g‘(x)=[-2f(x)+f’(x)]e^-2x＞0，故g(x)在[-2，2]上单调增加，从而

g(0)＞g’(-1)，

即

f(0)＞e²f(-1)，

又f(x)＞0，所以f(0)/f(-1)＞e²．选项(B)正确．同理可知选项(A)，(C)，(D)均不正确．

4.若可导函数f(x)满足f’(x)＜2f(x)，则当b＞a＞0时，有（ ）．(B)

A. b²f(a)＞a²f(b)

B. b²f(ln a)＞a²f(ln b)

C. b²f(a)＜a²f(b)

D. b²f(ln a)＜a²f(ln b)

解析：令ψ(x)=e^-2xf(x)，则由题设知，ψ’(x)=e^-2x[f’(x)-2f(x)]＜0，故ψ(x)单调减少．于是，当b＞a＞0时，ψ(ln b)＜ψ(ln a)，即e^{-2ln b}f(ln b)＜e^{-2ln a} f(ln a)，也即b^-2f(ln b)＜a^-2f(ln a)，由此即得b²f(ln a)＞a²f(ln b)．

由题干条件无法确定b²f(a)与a²f(b)的大小关系，如f(x)=e^x，则f’(x)=e^x＜2e^x=2f(x)．

令g(x)=e^x/x²(x＞0)，则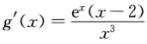

5.已知∫₁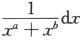^+∞(C)

A. a≤1

B. b≤1

C. a＞1

D. b＞1

解析：只需盯着x→+∞看，又由于a＞b＞0，因此原积分与∫₁^+∞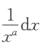

6.设f(x)为二阶可导函数，且x=0是f(x)的驻点，则二元函数z=f(x)f(y)在点(0，O)处取得极大值的一个充分条件是（ ）．(A)

A. f(0)＜0，f\\

B. f(0)＜0，f\\

C. f(0)＞0，f\\

D. f(0)=0，f\\

解析：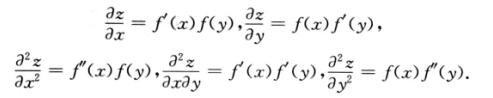

由于f’(0)=0，因此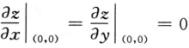，即点(0，0)是函数z=f(x)f(y)的驻点．在点(0，0)处，

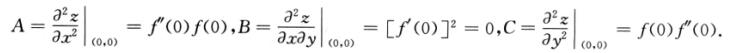
7.已知函数y=y(x)在任意点z处的增量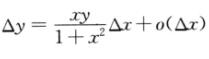，且y(0)=1，则y’(1)=（ ）．

本文档预览：3000字符，共12407字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载