
考研数学二(线性代数)模拟试卷101
选择题
1.设a,b,c是方程x3-2x+4=0的三个根,则行列式
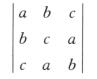 (B)
(B)
A. 1
B. 0
C. -1
D. -2
解析:方法一 由a,b,c是方程x3-2x+4=0的三个根,有
x3-2x+4=(x-a)(x-b)(x-c)
=x3-(a+b+c)x2+(bc+ac+ab)x-abc=0.
从而a+b+c=0,于是
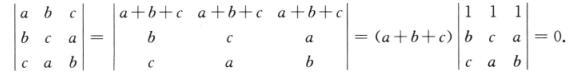
方法二 方程为x2-2x+4=(x+2)(x2-2x+2)=0.因a,b,c是方程x3-2x+4=0的三个根,不妨设a=-2,则b,c应满足x2-2x+2=0,由二次方程根与方程系数的关系,得b+c=-(-2)=2,因此有a+b+c=0.于是
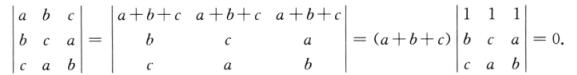
2.已知矩阵方程A=BC,其中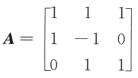 ,则B,C可以是( ).
,则B,C可以是( ).
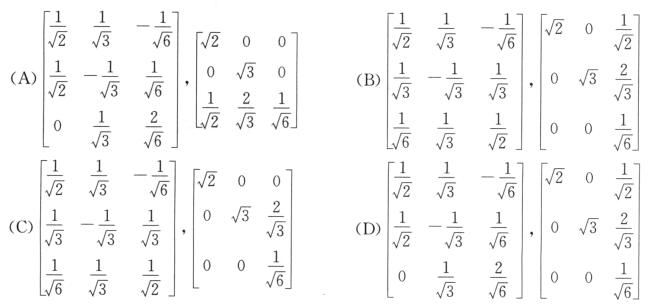
D
解析:在考研范围内,可认为本题考查矩阵相乘的运算规则.
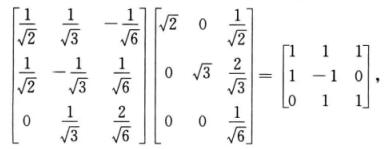
(D)选项符合题意.
事实上,(A)选项中左边矩阵第1行乘右边矩阵第1列得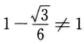 ,不符合题意,排除;
,不符合题意,排除;
(B),(C)选项中左边矩阵第3行乘右边矩阵第1列得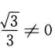
3.设A,B为3阶矩阵,且 (C)
(C)
A. 互换矩阵A-1的第1,2行得矩阵B
B. 互换矩阵A-1的第1,2列得矩阵B-1
C. 互换矩阵A的第1,2行得矩阵B-1
D. 互换矩阵A的第1,2列得矩阵B-1
解析:由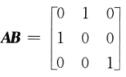 ,所以
,所以 =B-1,故互换矩阵A的第1,2行得矩阵B-1,选项C正确.
=B-1,故互换矩阵A的第1,2行得矩阵B-1,选项C正确.
现举例说明选项(A),(B),(D)不正确.
当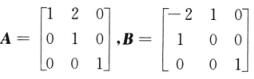 ,满足
,满足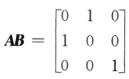
呼唤A-1= 的第1,2行得矩阵
的第1,2行得矩阵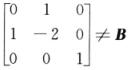 ,从而选项(A)不正确.
,从而选项(A)不正确.
互换A-1= 的第1,2列得矩阵
的第1,2列得矩阵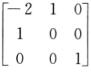 ≠B-1=
≠B-1= ,从而选项(B)不正确.
,从而选项(B)不正确.
互换矩阵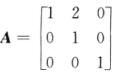 的第1,2列得矩阵
的第1,2列得矩阵 ≠B-1=
≠B-1=
4.设x1=[1,2,2,-4]T,x2=[1,k,-1,-4]T,x3=[-1,-3,1,k+6]T,则( ).(A)
A. 对任意常数k,x1,x2,x3线性无关
本文档预览:3000字符,共19910字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载