考研数学二（高等数学）模拟试卷158

考研数学二（高等数学）模拟试卷158

选择题

1.设f(x)连续，当x→0时，e^f(x)-1与x—ln(1+x)是等价无穷小量，以下结论：

①f(x)在x=0处取得极大值；

②(0，f(0))是曲线f(x)的拐点；

③f(x)在x=0处的2次泰勒多项式为(B)

A. 0

B. 1

C. 2

D. 3

解析：由题意，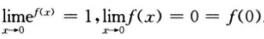

又当x→0时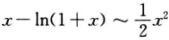，，故

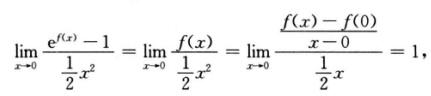
即f’(0)=0．又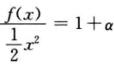，其中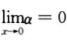，则f(x)=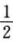x²+o(x²)，故f(x)在x=0处的2次泰勒多项式为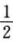

2.下列反常积分中发散的是（ ）．(C)

A. ∫₀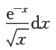^+∞B. ∫₀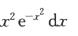^+∞C. ∫₀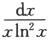^+∞D. ∫₀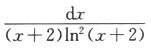^+∞解析：对于(A)选项，∫₀^+∞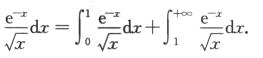

因为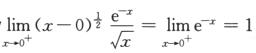，其中1/2<1，则∫₀¹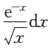收敛；

因为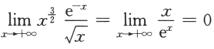，其中3/2＞1，则∫₀¹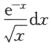收敛．

综上，∫₁^+∞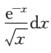

3.以函数y₁=xe^x，y₂=e^xsin x为特解的最低阶常系数齐次线性微分方程是（ ）．(D)

A. y”-3y”+4y’-2y=0

B. y’\\

C. y⁽⁴⁾-2y’\\

D. y⁽⁴⁾-4y’\\

解析：由题设知，所求微分方程的特征根为r₁=r₂=1，r_3,4=1±i，从而特征方程为

(r-1)²[r-(1+i)][r-(1-i)]=0，

即r⁴-4r³+7r²-6r+2=0，故所求微分方程为

y⁽⁴⁾-4y’\\

4.已知曲线y=y(x)上点P(x，y)(y≠0)处的法线与x轴，y轴的交点分别为Q，R，且|PR|=|RQ|，且C为任意常数，则曲线方程为（ ）．(A)

A. 2x²+y²=C

B. x²-2y²=C

C. x²+2y²=C

D. 2x²-y²=C

解析：由题设，曲线在点P(x，y)(y≠0)处的切线斜率为y’(x)(因为法线与两坐标轴均存在交点，所以斜率存在且不为0)，则法线的斜率为-1/y’(x)，法线方程为本文档预览：3000字符，共10724字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载