考研数学二（线性代数）模拟试卷106

考研数学二（线性代数）模拟试卷106

选择题

1.设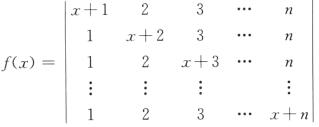，则f^(n-1)(0)=（ ）．

B

解析：由于

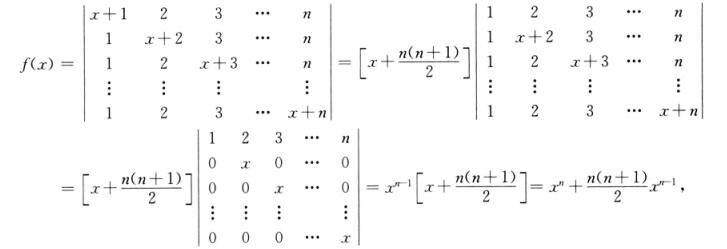
故f^(n-1)(x)=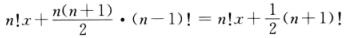，因此f^(n-1)(0)=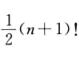

2.已知A为n阶矩阵，E为n阶单位矩阵，记矩阵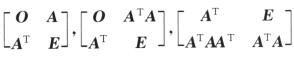(A)

A. r₁=r₂≥r₃

B. r₁=r₂≤r₃

C. r₁=r₃≥r₂

D. r₁=r₃≤r₂

解析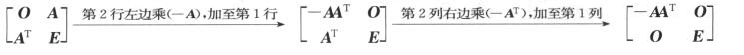：，故r₁=r(-AA^T)+n．

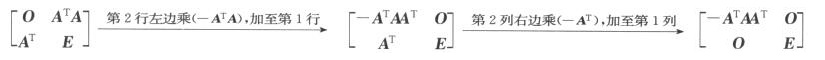，故r₂=r(-A^TAA^T)+n.

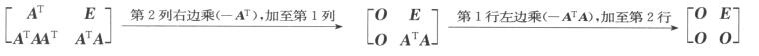
3.设向量α₁=[1，1，2]^T，α₂=[2，a，4]^T，α₃=[a，3，6]^T，α₄=[0，2，2a]^T，若向量组α₁，α₂，α₃，α₄与α₁，α₂，α₃不等价，则a=（ ）．(B)

A. 2

B. 3

C. 4

D. 6

解析：[α₁，α₂，α₃|α₄]=

4.设A为m×n矩阵，e=[1，1，…，1]^T．若方程组Ay=e有解，则对于(I)A^Tx=0与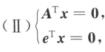(D)

A. (I)的解都是(Ⅱ)的解，但(Ⅱ)的解未必是(I)的解

B. (Ⅱ)的解都是(I)的解，但(I)的解未必是(Ⅱ)的解

C. (I)的解不是(Ⅱ)的解，且(Ⅱ)的解也不是(I)的解

D. (I)的解都是(Ⅱ)的解，且(Ⅱ)的解也都是(I)的解

解析：显然方程组(Ⅱ)的解都是方程组(I)的解．由Ay=e有解，知r(A)=r([A，e])，于是r(A^T)=r([A，e]^T)=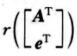

5.设A是3阶矩阵，Ax=0有通解k₁ξ₁+k₂ξ₂(k₁，k₂为任意常数)，Aξ₃=ξ₃，则存在可逆矩阵P，使P^-1AP=(C)

A. [ξ₁，ξ₂，ξ₁+ξ₃]

B. [ξ₂，ξ₃，ξ₁]

C. [ξ₁+ξ₂，-ξ₂，2ξ₃]

D. [ξ₁+ξ₂，ξ₂-ξ₃，ξ₃]

解析：ξ₁，ξ₂是A的对应于λ₁=λ₂=0的线性无关的特征向量，ξ₃是A的对应于λ₃=1的特征向量，且注意下列性质：

①对A的同一个特征值对应的特征向量，如ξ₁，ξ₂是λ=0对应的特征向量，则k₁ξ_{1本文档预览：3000字符，共13175字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载}