管理类专业学位联考综合能力（数学）模拟试卷68

管理类专业学位联考综合能力（数学）模拟试卷68

管理类专业学位联考（综合能力）-问题求解

1.若a+3b=0，则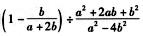(A)

A. 5／2

B. 3／2

C. 7／2

D. 1／2

E. 9／2

解析：本题不可能求出a，b的值，应利用a+3b=0找出a，b之间的关系解答．

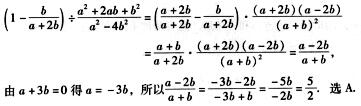
2.如果买6根铅笔的价钱等于买5块橡皮的价钱，而买6块橡皮要比买5根铅笔多花1．1元，则一块橡皮比一根铅笔多( )元．(A)

A. 0．1

B. 0．2

C. 0．3

D. 0．5

E. 0．4

解析：已知6铅笔=5橡皮，6橡皮－5铅笔=1橡皮+1铅笔=1．1(元)，

得到：1铅笔=0．5(元)，1橡皮=0．6(元)．因此，1橡皮－1铅笔=0．1(元)，选A．

3.已知两个自然数的积为240，最小公倍数为60，这两个自然数最大相差( )．(D)

A. 3

B. 21

C. 36

D. 56

E. 58

解析：设这两个数为a与b，a＜b，且设(a，b)=d，a=da₁，b=db₁，其中(a₁，b₁)=1．

因为“两个自然数的积=两数的最大公约数×两数的最小公倍数”，因此240=d·60．

解出d=4，因此a=4a₁，b=4b₁．

因为a与b的最小公倍数为60，所以4a₁b₁=60，于是有a₁b₁=15．

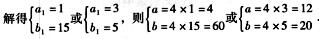
4.有一个200米的环形跑道，甲、乙两人同时从同一地点同方向出发．甲以0．8米／秒的速度步行，乙以2．4米／秒的速度跑步，乙在第2次追上甲时用了( )秒．(D)

A. 200

B. 210

C. 230

D. 250

E. 280

解析：乙第二次追上甲，比甲多跑两圈，时间为200×2／(2．4－0．8)=250(秒)，选D．

5.把整数部分是0，循环节有三位数字的纯循环小数化成最简分数后，如果分母是一个两位数的质数，那么这样的最简真分数有( )个．(E)

A. 37

B. 32

C. 29

D. 35

E. 36

解析：三位循环节的纯循环小数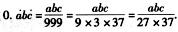

6.如图所示，直角梯形ABCD的上底是5，下底是7，高是4，且△ADE，△ABF和四边形AECF的面积相等，则△AEF的面积是( )．

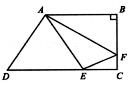(C)

A. 5．6

B. 5．8

C. 6．8

D. 1．2

E. 6．2

解析：梯形面积为(5+7)×4÷2=24，故S_△ABF=S_△ADE=8，求得

BF=3．2，DE=4，CF=0．8，CE=3，

故S_△CEF=1．2，剩余S_△AEF=6．8，选C．

7.已知三个不等式：①x²－4x+3＜0，②x²－6x+8＜0，③2x²－9x+m＜0．要使满足式①和式②的所有x都满足式③，则实数m的取值范围是( )．(C)

A. m＞9

B. m＜9

C. m≤9

D. 0＜m≤9

E. m=9

解析：由式①得1＜x＜3，由式②得2＜x＜4，联合式①和式②，则2＜x＜3．

所有满足2＜x＜3的x都满足式③，用抛物线画图法，必须满足f(2)≤0，且f(3)≤0．注意可以取到等号，求得m≤9．选C．

8.一种细胞每三分钟分裂一次(一次分裂为两个)，把一个这种细胞放入一个容器内，恰好一小时充满容器；如果开始时把两个这种细胞放入该容器内，那么细胞充满容器的时间为( )分钟．(A)

A. 57

B. 30

C. 27

D. 45

E. 54

解析：三分钟分裂一次．初始容器内有两个细胞时，相当于比原来少分裂一次，所以是57分钟，选A．

9.已知数列{a_n}的通项公式为a_n=2ⁿ，数列{b_n}的通项公式为b_n=3n+2．若数列{a_n}和{b_n}的公共项按顺序组成数列{c_n}，则数列{c_n}的前三项之和为( )．(B)

A. 248

B. 168

C. 128

D. 198

E. 218

解析：求解{a_n}和{b_n}的公共项，相当于求解a_n=b_m，其中m和n都是正整数．数列{b_n本文档预览：3000字符，共10776字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载