管理类专业学位联考综合能力（数学）模拟试卷111

管理类专业学位联考综合能力（数学）模拟试卷111

管理类专业学位联考（综合能力）-问题求解

1.不等式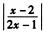(A)

A. x＜－1或x＞1

B. x≤－1

C. x＞1

D. －1＜x＜1

E. x＜－2或x＞2

解析：

2.若不等式|x－4|+|3－x|＜a的解集为空集，则a的取值范围为( )．(B)

A. a≥4

B. a≤1

C. a≤3

D. a＜1

E. 3＜a≤4

解析：由|x－4|+|3－x|的最小值为1可得，当a＞1时，|x－4|+|3－x|＜a有解；当a≤1时，原不等式解集为空集．

3.甲、乙、丙三人，每分钟分别行68米、70．5米、72米．现甲、乙从A镇去B镇，丙从B镇去A镇，三人同时出发，丙和乙相遇后，又过2分钟与甲相遇．则乙丙相遇时间为( )分钟．(C)

A. 80

B. 96

C. 112

D. 120

E. 140

解析：乙、丙两人相遇时，乙比甲多行的路程正好是后来甲、丙2分钟所走的路程和，是(68+72)×2=280(米)．每分钟乙比甲多行70．5－68=2．5(米)．可知乙、丙相遇时间是280÷2．5=112(分钟)．

4.一件工程要在规定时间内完成．若甲单独做要比规定的时间推迟4天完成，若乙单独做要比规定的时间提前2天完成．若甲、乙合作了3天，剩下的部分由甲单独做，恰好在规定时间内完成，则规定时间为( )天．(B)

A. 19

B. 20

C. 21

D. 22

E. 24

解析：根据题意可知，甲做4天的量等于乙做3天的量，那么完成任务的时间之比为4∶3．而1份的量恰好等于6天，所以甲单独完成需要24天，乙单独完成需要18天，计划时间为24－4=18+2=20(天)．

5.(D)

A.

B.

C.

D.

E.

解析：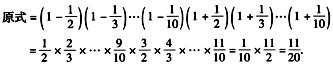

6.已知不等式(m²+4m－5)x²－4(m－1)x+3＞0对一切实数x恒成立，则实数m的取值范围为( )．(E)

A. 1＜m≤19

B. 1≤m＜18

C. 1＜m＜19

D. 1≤m≤18

E. 1≤m＜19

解析：依题意，①当m²+4m－5=0时，m=1或m=－5，当m=1时，原不等式化为3＞0，恒成立；当m=－5时，不合题意．

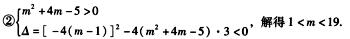
7.设n是自然数，且n²+15n+26是一个完全平方数，则n的值为( )．(B)

A. 21

B. 23

C. 25

D. 27

E. 36

解析：令n²+15n+26=m²(m∈Z₊)方程n²+15n+26－m²=0有整数解，那么判别式为完全平方数，令Δ=k²(k∈Z₊)，故Δ=225－4(26－m²)=k²k²－4m²=121(k+2m)(k－2m)=121，因为很明显m²≥26，所以k+2m≠k－2m，那么可得出故k=61，m=30，代入原方程中，有n²+15n－874=(n－23)(n+38)=0

8.如图9-1所示，在△ABC，∠BAC=90°，AC＞AB，AD是高，M是BC的中点，BC=8，DM=，则AD的长度为( )．

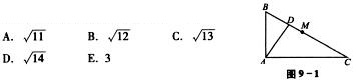(C)

A.

B.

本文档预览：3000字符，共12050字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载