管理类专业学位联考综合能力（数学）模拟试卷112

管理类专业学位联考综合能力（数学）模拟试卷112

管理类专业学位联考（综合能力）-问题求解

1.对任意实数x，若不等式|x+1|－|x－2|＞k恒成立，则k的取值范围为( )．(C)

A. k＞－3

B. k≤3

C. k＜－3

D. k＜3

E. k≤－3

解析：根据绝对值的几何意义，设数x，－1，2在数轴上对应的点分别为P，A，B，则原不等式等价于|PA|－|PB|＞k恒成立．因为|AB|=3，即|x+1|－|x－2|≥－3，故当k＜－3时，原不等式恒成立．

2.甲、乙、丙三人同时从起点出发进行1000米自行车比赛(假设他们各自的速度保持不变)，甲到终点时，乙距终点还有40米，丙距终点还有64米．那么乙到达终点时，丙距终点( )米．(B)

A. 21

B. 25

C. 30

D. 35

E. 39

解析：当甲到达终点这个时刻时，s_乙∶s_丙=v_乙∶v_丙=960∶936=40∶39．那么当乙到达终点时，比例并没有改变，所以1000米仍然为40份，丙距终点还有1份，为1000÷40=25(米)．

3.加工一批零件，甲、乙合作24天可以完成；由甲先做16天，然后由乙再做12天后，还剩下这批零件的2／5没有完成．已知甲每天比乙多加工3个零件，则这批零件共有( )个．(C)

A. 120

B. 240

C. 360

D. 480

E. 600

解析：首先求甲、乙合作12天后，完成了总量的，那么甲多干4天的量相当于完成总量的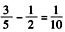那么乙的效率为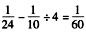；最后求出这批零件的个数为：3÷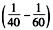

4.S_n=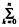(B)

A. 1

B. －1

C. 2

D. －2

E. 3

解析：依题意，有S₁₀₀=1－3+5－7+…+197－199+201=－2×50+201=101，S₁₀₁=1－3+5－7+…+201－203=－2×51=－102，所以S₁₀₀+S₁₀₁=－1．

5.已知函数f(x)=x²+ax+b在区间[0，2]上有两个零点，则2a+b的最小值为( )．(D)

A. －1

B. －2

C. －3

D. －4

E. 0

解析：设两个零点为x₁，x₂，则x₁+x₂=－a，x₁x₂=b，所以2a+b=－2(x₁+x₂)+x₁x₂=(2－x₁)(2－x₂)－4，根据两零点的已知范围易得，2a+b的最小值为－4．

6.当x∈(1，2)时，不等式x²+mx+4＜0恒成立，则m的取值范围是( )．(C)

A. m≥－5

B. m＜－5

C. m≤－5

D. m＜－1

E. －10≤m≤－5

解析：构造函数：f(x)=x²+mx+4．由于当x∈(1，2)时，不等式x²+mx+4＜0恒成立．所以f(1)≤0，f(2)≤0，即1+m+4≤0，4+2m+4≤0．解得m≤－5．

7.方程6xy+4x－9y－7=0的整数解有( )种情况．(A)

A. 1

B. 2

C. 3

D. 4

E. 0

解析：原式6xy+4x－9y－7=0可化简为(2x－3)(3y+2)=1，故讨论可得只有1组整数解，选A．

已知等差数列{a_n}的公差d=1／2，S₁₀₀=145．设S_奇=a₁+a₃+a₅+…+a₉₉，S\’=a₃+a₆+a₉+…+a₉₉．

8.S_奇=( )．(C)

A. 51

B. 57

C. 60

D. 64

E. 66

解析：依题意，可得S_奇+S_偶=145，即S_奇+(S_奇+50d)=145，即2S_奇+25=145，解得S_奇=60．

9.S’=( )。(B)

A. 45．2

B. 56．1

C. 54．2

D. 58．1

E. 59．1

解析：由S₁₀₀=145，得本文档预览：3000字符，共10661字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载