考研数学（数学二）模拟试卷749

考研数学（数学二）模拟试卷749

选择题

1.已知f(x)具有二阶连续导数，g(x)为连续函数，且f’(x)=ln (1+x²)+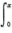g(x-t)dt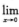，(C)

A. x=0为f(x)的极大值点.

B. x=0为f(x)的极小值点.

C. (0，f(0))为曲线y=f(x)的拐点.

D. x=0不是f(x)的极值点，(0，f(0))也不是曲线y=f(x)的拐点.

解析：先计算出f’(0)，f”(0)，f”’(0)等，然后再确定是极值点还是拐点．由f’(x)=ln (1+x²)+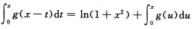

有F”(x)=2x／(1+x²)+g(x).

于是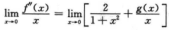=2+3=5.

进而可推出f”(0)=0，f”’(0)=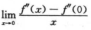

2.设函数f(x)=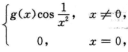(D)

A. 连续但不可导.

B. 可导但f’(0)≠0.

C. 极限存在但不连续.

D. 可微且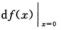解析：在分段点的极限、连续、导数应根据定义讨论.

由g’(0)=0知g(x)在x=0处可导，也可知g(x)在x=0处连续，即

3.已知级数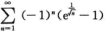ln(1+1／n^α)绝对收敛，级数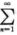(C)

A. α＞5／2.

B. 2＜α＜3.

C. 1／2＜α＜1.

D. α＜3.

解析：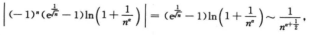

由级数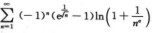绝对收敛，则α+1／2＞1，即α＞1／2

级数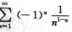

4.设平面区域D由x=0，y=0，2x+y=1／3，2x+y=1围成，若I₁=ln⁵(2x+y)dxdy，I₂=(2x+y) ⁵dxdy，I₃=(B)

A. I₁＜I₂＜I₃.

B. I₁＜I₃＜I₂.

C. )I₃＜I₂＜I₁.

D. I₃＜I₁＜I₂–

解析：利用二重积分的性质.由1／3≤2x+y≤1，x＞0，y＞0知，ln(2x+y)≤0.又可知0＜2x+y＜π／2，sin(2x+y)＜2x+y.所以ln(2x+y)≤0≤sin(2x+y)≤2x+y，

从而在区域D内ln⁵(2x+y)≤sin⁵ (2x+y)≤(2x+y) ⁵从而

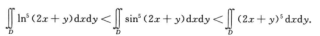
5.设向量组α₁，α₂线性无关，t为常数，则下列向量组必线性无关的是(B)

A. α₁，α₁+tα₂.

B. α₁，tα₁+α₂.

C. tα₁-α₂，α₁+α₂.

D. tα₁，α₁+tα₂.

解析：首先我们有结论：若向量组α₁，α₂线性无关，且(k₁₁α_1<

本文档预览：3000字符，共13589字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载