考研数学（数学二）模拟试卷753

考研数学（数学二）模拟试卷753

选择题

1.设f(x)满足2f(x)+f(2-x)=lnx，则y=f(x)在点(1，f(1))的切线方程为(C)

A. y=x／2.

B. y=-x／2

C. y=x-1.

D. y=-x.

解析：因为2f(t)+f(2-t)=lnt，令t=2-x可知2f(2-x)+f(x)=ln(2-x).联立方程

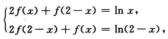
2.若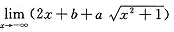(A)

A. a=2，b=-1.

B. a=2，b=1.

C. a=-2，b=-1.

D. a=-2，b=1.

解析：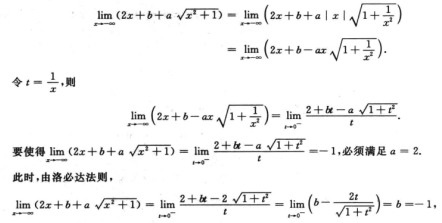

3.设f(x)=x²／2-2xarctanx+ln (1+x²)，则(B)

A. y=f(x)的图形的凸区间为(-∞，0)，(1，+∞)，凹区间为(0，1)．

B. y=f(x的图形的凸区间为(-1，1)，凹区间为(-∞，-1)，(1，+∞).

C. y=f(x的图形的凸区间为(-∞，1)，凹区间为(1，+∞)．

D. y=f(x的图形的凸区间为(-∞，-1)，凹区间为(-1，+∞).

解析：f(x)=x²／2-2xarctanx+ln(1+x²)在实轴上有定义.f’(x)=x-2arctanx，F”(x)=(x²-1)／(1+x²).当x∈(-1，1)时，f”(x)＜0，y=f(x)的图形是凸的；当x∈(-∞，-1)或x∈(1，+∞)时，f”(x)＞0，y=f(x)的图形是凹的.所以(B)为正确选项.

4.已知曲线y=y(x)经过原点，且在原点的切线平行于直线2x-y-5=0，而y(x)满足y”-6y’+9y=e^3x，则y(x)等于(C)

A. sin2x.

B. 1／2x²e^2x+sin2x.

C. x／2(x+4)e^3x.

D. (x²cosx+sin2x)e^3x

解析：微分方程y”-6y’+9y=e^3x对应的齐次方程的特征根为λ₁=λ₂=3,

因此齐次方程的通解为y₀(x)=(C₁+C₂x)e^3x.

设非齐次方程的特解为y^*=Ax²e^3x，代入y”-6y’+9y=e^3x，可求得A=1／2，

所以原微分方程的通解为y(x)=(C₁+C₂x)e^3x+1／2x²e^3x.

已知曲面y=y(x)经过原点，所以C₁=0.

又因为在原点切线平行于直线2x-y-5=0，所以y’(0)=2，则有C₂=2.

故通解为y(x)=2xe^3x+1／2x²e^3x=x／2(x+4)e^3x，选择(C).

5.已知α=(1，-3，2)^T，β=(0，1，-1)^T，矩阵A=2βα^T+7E，则矩阵A的最小特征值的特征向量是(B)

A. α.

B. β.

C. α+β.

D. α-β.

解析：令B=βα^T，则秩r(B)=1.

由α^Tβ=-5，知矩阵B的特征值是-5，0，0．

那么矩阵A=2B+7E的特征值是-3，7，7．

矩阵B关于λ=-5的特征向量就是矩阵A关于λ=-3的特征向量.

而Bβ=(βα^T)β=β(α^Tβ)=-5β，

所以应选(B).

6.设矩阵A=(α₁，α₂，α₃，α₄)是5×4矩阵，η₁=(1，2，-1，3)^T，η₂=(3，2，5，3)^T是齐次线性方程组Ax=0的基础解系.下列命题中错误的是(C)

A. α₁，α₂，α₃线性相关.

B. α₃，α₄线性无关.

C. a=可由α₁，α₃线性表示.

D. α₂可由α₃，α₄线性表示.

解析：A是5×4矩阵，齐次方程组Ax=0的基础解系有两个向量，故n-r(A)=2，即r(A)=r(α₁，α₂，α₃，α₄)=2.故(A)必正确.

由Aη₁=0，Aη₂=0可得

α₁+2α₂-α₃+3α₄=0，3α₁+2α₂+5α₃+3α₄=0，

两式分别相减、相加可得

α₁+3α₃=0，2α₁+2α_{2本文档预览：3000字符，共12738字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载}