
考研数学(数学二)模拟试卷750
选择题
1.当x→0+时,下列无穷小量中最高阶的是
 (D)
(D)
A.
B.
C.
D.
解析:本题要用一个基本结论:若f(x)在x=0的某邻域内连续,且当x→0时,f(x)是x的m阶无穷小,φ(x)是x的n阶无穷小,则F(x)=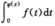 是x的n(m+1)阶无穷小.由此可知
是x的n(m+1)阶无穷小.由此可知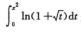 是x的2×(1/2+1)=3阶无穷小.
是x的2×(1/2+1)=3阶无穷小.
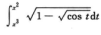 的上下限不同阶,则其阶数由低阶的x2和被积函数的阶数所决定,
的上下限不同阶,则其阶数由低阶的x2和被积函数的阶数所决定,
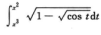 是x的2×(1+1)=4阶无穷小.
是x的2×(1+1)=4阶无穷小.
 的上下限同阶但不等价,则其阶数可由上下限中任一个和被积函数的阶数所决定,
的上下限同阶但不等价,则其阶数可由上下限中任一个和被积函数的阶数所决定,
 是x的1×(2+1)=3阶无穷小.
是x的1×(2+1)=3阶无穷小.
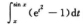 的上下限是等价无穷小,此时,其阶数不能由上下限和被积函数的阶数所确定.由于
的上下限是等价无穷小,此时,其阶数不能由上下限和被积函数的阶数所确定.由于
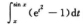 =(sinx-x)(eξ2 -1),
=(sinx-x)(eξ2 -1),
其中ξ介于x与sinx之间.当x→0+时,eξ2-1是x的2阶无穷小,又sinx-是x的3阶无穷小,则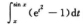
2.设f(x)连续且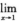 f(x)-1/(x-1)=2,则
f(x)-1/(x-1)=2,则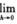 (D)
(D)
A. 0.
B. 2.
C. 4.
D. 8.
解析:由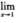 f(x)-1/x-1=2,得f(1)=1,f’(1)=2.
f(x)-1/x-1=2,得f(1)=1,f’(1)=2.
则
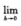 f2(1+h)-f2(1-h)/h=
f2(1+h)-f2(1-h)/h=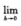 f(1+h)-f(1-h)/h[f(1+h)+f(1-h)]
f(1+h)-f(1-h)/h[f(1+h)+f(1-h)]
=2f(1)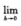
3.设D={(x,y)|x2+y2≤14则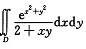
D
解析: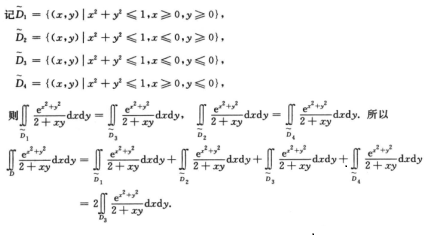
4.已知级数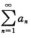 =2,且
=2,且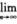 nan=0,则
nan=0,则 (B)
(B)
A. 0.
B. 2.
C. -2.
D. 4.
解析:用级数收敛的定义,部分和
Sn=
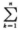 k(ak -a k+1)
k(ak -a k+1)
=(a1-a2)+2(a2-a3)+3(a3-a4)+
…+(n-1)(an-1-an)+n(an-an+1)
=a1+a2+a3+…+
本文档预览:3000字符,共15746字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载
