管理类专业学位联考综合能力（数学）模拟试卷104

管理类专业学位联考综合能力（数学）模拟试卷104

管理类专业学位联考（综合能力）-问题求解

1.设实数x，y满足|3x|+|2y|≤1，则x²+y²+2y的最小值为( )．

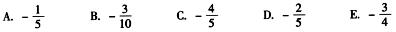(E)

A.

B.

C.

D.

E.

解析：x²+y²+2y=x²+(y+1)²－1可以看成(0，－1)点到|3x|+|2y|≤1的距离d的平方再减1的数值，如图1-18所示；故最小值为d_min²－1=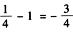选E．

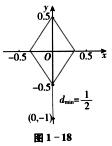
2.甲、乙两车分别从A、B两地同时出发相向而行，8小时后在C点相遇．如果甲车速度不变，乙车每小时多行5千米，且两车还从A、B两地同时出发相向而行，则相遇点距C点16千米．如果乙车速度不变，甲车每小时多行5千米，且两车还从A、B两地同时出发相向而行，则相遇点距C点20千米．A、B两地之间的距离为( )千米．(E)

A. 280

B. 300

C. 320

D. 340

E. 360

解析：一个是甲的速度增加5千米／小时，一个是乙的速度增加5千米／小时，知道甲、乙速度和不变(v₁+v₂)，所以两次速度增加以后的速度和一样(v₁+v₂+5)，相遇时间也一样．

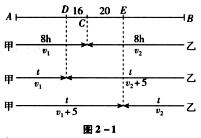
如图2-1所示，可以得到速度增加后的相遇时间

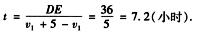
对于甲来说，原来速度不增加时，8小时可以到达C点，

得到甲的速度v₁=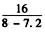=20(千米／小时)，

乙的速度v₂=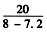

3.加工一个零件，甲需3分钟，乙需3．5分钟，丙需4分钟．现有1825个零件要加工，为尽早完成任务，甲、乙、丙各加工一定数量零件，那么完成任务所需时间最少是( )．(D)

A. 24小时

B. 28小时

C. 32小时

D. 35小时

E. 36小时

解析：三人同时加工，并且同一时间完成任务，所用时间最少，要同时完成，应根据工作效率之比，按比例分配工作量．

三人工作效率之比是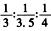=28∶24∶21，则他们分别需要完成的工作量是：

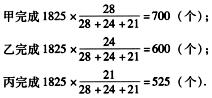
4.有三块草地，面积分别为5公顷、6公顷和8公顷．草地上的草一样厚，而且长得一样快．第一块草地可供11头牛吃10天，第二块草地可供12头牛吃14天．则第三块草地可供19头牛吃( )天．(D)

A. 5

B. 6

C. 7

D. 8

E. 9

解析：看到有三块不同的草地，只需将三块草地的面积统一起来，即[5，6，8]=120．

这样，第一块草地5公顷可供11头牛吃10天变成120公顷可供264头牛吃10天；

第二块草地可供12头牛吃14天变成可供240头牛吃14天；

那么120公顷的草地每天的生长量为(240×14－264×10)÷(14－10)=180(份)；

120公顷的草地原来有草：(240－180)×14=840(份)；

第三块草地变成120公顷供285头牛吃多少天的问题了，那么需要840÷(285－180)=8(天)．

5.已知x=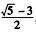(B)

A. －2

B. －1

C. 2

D. 1

E. 3

解析：由x=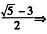(2x+3)²=5x²+3x+1=0

6.如果函

本文档预览：3000字符，共15768字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载