管理类专业学位联考综合能力（数学）模拟试卷107

管理类专业学位联考综合能力（数学）模拟试卷107

管理类专业学位联考（综合能力）-问题求解

1.方程||x－2|－1|=a(0＜a＜1)的所有解之和为( )．(C)

A. 8－2a

B. 8+2a

C. 8

D. －8

E. 2a

解析：当x≥2时，||x－2|－1|=|x－2－1|=|x－3|=a，得x=3+a或x=3－a．

当x＜2时，||x－2|－1|=|2－x－1|=|1－x|=a，得x=1+a或x=1－a．

则所有解之和为8，选C．

2.已知x=2010，则|4x²－5x+1|－4|x²+2x+2|+3x+7的值为( )．(C)

A. 20100

B. 20200

C. －20100

D. －20200

E. 20300

解析：当x=2010时，原式=4x²－5x+1－4(x²+2x+2)+3x+7=－10x=－20100．

3.两辆汽车同时从A，B两站相向开出．第一次在离A站60千米的地方相遇．之后，两车继续以原来的速度前进．各自到达对方车站后都立即返回．又在距中点右侧30千米处相遇．A，B两站相距( )千米．(E)

A. 110

B. 120

C. 130

D. 150

E. 140

解析：两车第一次相遇共走了s千米，假设所用时间为t小时，此时一辆汽车走了60千米；当第二次相遇的时候，两车共走了3s千米，在速度不变的前提下，那么所用时间应当为3t小时，这辆汽车总共走了就是180千米，那么可以得到180=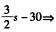

4.粗蜡烛和细蜡烛长短一样．粗蜡烛可以点5小时，细蜡烛可以点4小时．同时点燃这两支蜡烛，点了一段时间后，粗蜡烛长是细蜡烛长的2倍这两支蜡烛点了( )小时．

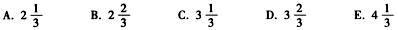(C)

A.

B.

C.

D.

E.

解析：假设两根蜡烛的长度均为20份，那么粗蜡烛一小时可以燃烧4份，细蜡烛一小时可以燃烧5份．设点了x小时。那么根据题意有20－4x=2(20－5x)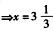

5.抛物线y=ax²+bx+c的图像与x轴有两个交点M(x₁，0)，N(x₂，0)，且经过点A(0，1)，其中0＜x₁＜x₂．过点A的直线l与x轴交于点C，与抛物线交于点B(异于点A)，满足△CAN是等腰直角三角形，且S_△BMN=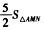(D)

A. 6

B. 7

C. 8

D. 10

E. 12

解析：由条件知该抛物线开口向上，与x的两个交点在y轴的右侧．

由于△ACN是等腰直角三角形，故点C在x轴的左侧，且∠CAN=90°．

故∠ACN=45°，从而C(－1，0)，N(1，0)．于是直线l的方程为y=x+1．

设B(X₃，y₃)，由S_△AMN=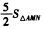知y₃=5／2，从而x₃=3／2，即B(3／2，5／2)．

综上可知，该抛物线通过点A(0，1)，B(3／2，5／2)，N(1，0)．

于是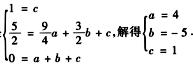

6.若a，b，c为正实数，且a+b+c=4，则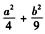(C)

A. 1

B. 3／2

C. 8／7

D. 2

E. 4

解析：由权方和不等式可得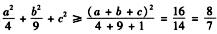

7.设等差数列{a_n}的公差d不为0，a₁=9d，若a_k是a₁与a_2k的等比中项，则k=( )．(B)

A. 2

B. 4

C. 6

D. 8

E. 10

解析：由a_k是a₁与a_2k的等比中项，可得a_k²=a₁a_2k，由{a_n}为等差数列可得

a_k=a₁+(k－1)d，a_2k=a₁+(2k－1)d，

又a₁=9d，代入可得k=4．

8.如图9-24所示，在Rt△ABC中，∠AC

本文档预览：3000字符，共12397字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载