中学教师资格认定考试（高级数学学科知识与教学能力）模拟试卷59
单项选择题
1.已知函数z=x2+3xy+2x+y，则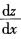
(B)
A. 2x+3y
B. 2x+3y+2
C. 3x+1
D. 2x+1
解析：根据二元函数偏导数的定义，求函数z(x，y)关于z的导数，将y看作常数，只对x求导即可，所以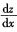
2.方程y2=2－x表示空间的曲面为( )。(D)
A. 球面
B. 旋转双曲面
C. 圆锥面
D. 抛物柱面
解析：球面的标准方程为(x－a)2+(y－b)2+(z－c)2=r2。旋转双曲面的方程：单叶双曲面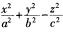
=1，双叶双曲面
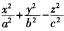=－1。圆锥面方程为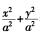
3.若A是m×n阶矩阵，且A的n个列向量线性无关，则A的秩( )。(D)
A. 大于n
B. 大于m
C. 等于m
D. 等于n
解析：矩阵A的n个列向量线性无关，所以矩阵A的列向量的秩等于n，根据矩阵的秩等于列向量的秩，也等于行向量的秩，所以r(A)=n，故本题选D。
4.设随机变量ξ服从标准正态分布N(0，1)，下列命题正确的是( )。
(1)P(｜ξ｜＜a)=P(｜ξ｜＜a)+P(｜ξ｜=a)(a＞0)；
(2)P(｜ξ｜＜a)=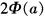
－1(a＞0)；
(3)P(｜ξ｜＜a)=1－
(C)
A. (2)(4)
B. (3)(4)
C. (1)(2)(4)
D. (1)(2)(3)(4)
解析：因为连续型随机变量在离散点处的概率为0，即P(｜ξ｜=a)=0(a＞0)，所以当a＞0时，P(｜ξ｜＜a)=P(｜ξ｜＜a)+P(｜ξ｜=a)，P(｜ξ｜＜a)=1－P(｜ξ｜≥a)=1－P(｜ξ｜＞a)，故(1)(4)正确。当a＞0时，P(｜ξ｜＜a)=P(－a＜ξ＜a)=P(ξ＜a)－P(ξ＜－a)=P(ξ＜a)－(1－P(ξ＜a))=2P(ξ＜a)－1=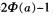
5.下列数列收敛的是( )。
B
解析：A项中，当n→∞时，{(－1)n}的极限不存在，该数列发散；B项中，因为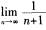
=0，所以数列
收敛；C项和D项中，因为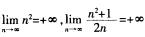
，所以数列{n2}和数列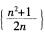
6.设A=
(A)
A. (1，2，3)T
B. (1，2，0)T
C. (2，1，3)T
D. (0，1，－3)T
解析：首先，求矩阵A的特征值，如下：
｜λE－A｜=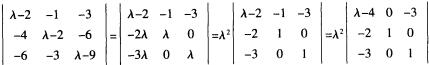
=λ2(λ－13)=0，解得λ=0(二重)或13。
当λ=0时，(OE－A)=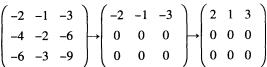
，可知矩阵A特征值为0时，所对应的两个线性无关的特征向量为(－1，2，0)T，(－3，0，2)T，经验证，选项中的向量均不能由这两个向量线性表出。
当λ=13时，(13E－A)=
7.希腊数学的历史可以
本文档预览：3000字符，共11385字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
