中学教师资格认定考试（高级数学学科知识与教学能力）模拟试卷60

中学教师资格认定考试（高级数学学科知识与教学能力）模拟试卷60

单项选择题

1.级数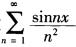(B)

A. 条件收敛

B. 绝对收敛

C. 发散

D. 无法判别

解析：因为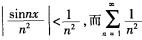为p级数，p=2＞1，级数收敛。所以级数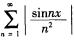收敛，故级数

2.方程组(D)

A. －1

B. ±1

C. 0

D. 1

解析：齐次线性方程组有非零解，则其系数矩阵的秩小于未知数个数，对应的系数矩阵的行列式为0，即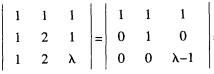

3.在空间右手直角坐标系中，向量α，β，γ的坐标依次为(1，0，－1)，(1，－2，0)，(－1，2，1)，则(3α+β－γ)×(α－β+γ)的坐标为( )。(A)

A. (16，4，16)

B. (16，－4，16)

C. (－16，4，16)

D. (16，4，－16)

解析：3α+β－γ的坐标为(5，－4，－4)，α－β+γ的坐标为(－1，4，0)，所以(3α+β－γ)×(α－β+γ)=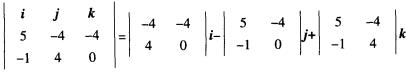

4.设三阶方阵A的特征值为1，2，－3，则｜A²－3A－E｜的值为( )。(B)

A. 135

B. 153

C. －6

D. 0

解析：由矩阵特征值的性质可知，如果λ是矩阵A的一个特征值，则λ²是A²的特征值，kλ是kA的特征值，λ－1是A－E的特征值。所以矩阵A²－3A－E的特征值为λ²－3λ－1(其中λ=1，2，－3)，即为－3，－3，17。因为矩阵的行列式等于矩阵所有特征值的乘积，所以｜A²－3A－E｜=(－3)×(－3)×17=153。

5.设随机变量X服从二项分布B(n，p)，则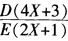的值为( )。

(C)

A.

B.

C.

D.

解析：因为随机变量X服从二项分布B(n，P)，所以E(X)=np，D(X)=np(1－p)，进而根据期望和方差的性质D(aX+b)=a²D(X)，E(aX+b)=aE(X)+b知，D(4X+3)=16D(X)=16np(1－p)，E(2X+1)=2E(X)+1=2np+1，所以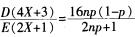

6.下列命题正确的个数是( )。

(1)若f(x)是[a，b]上的连续函数，则f(x)在[a，b]上可导；

(2)若函数f(x)在[a，b]上可导，则f(x)是[a，b]上的连续函数；

(3)“函数f(x)在[a，b]上可导”是“函数f(x)在[a，b]上可微”的充要条件；

(4)若f(x)是(a，b)内的连续函数，则f(x)在(a，b)内可积；

(5)若函数f(x)在[a，b]上有界，且只有有限个间断点，则f(x)在[a，b]上可积。(B)

A. 2

B. 3

C. 4

D. 5

解析：一元函数在闭区间上可导一定连续，但在闭区间上连续不一定可导，所以(1)错误，(2)正确。“函数f(x)在[a，b]上可导”的充要条件是“函数f(x)在[a，b]上可微”，所以(3)正确。一元函数在开区间内连续，不一定可积，例如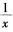在(0，1)内连续，但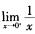=+∞，其在(0，1)内不可积，所以(4)错误。一元函数在闭区间上连续或在闭区间上有界且只有有限个间断点，则一定可积，但可积不一定连续，所以(5)正确。故本题选B。

一元函数在闭区间上可积、可导、可微、连续的关系图如下：

7.提出“一笔画定理”的数学家是( )。(C)

A. 高斯

B. 牛顿

C. 欧拉

D. 莱布尼兹

解析：欧拉通过对七桥问题的研究提

本文档预览：3000字符，共9412字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载