考研数学（数学二）模拟试卷744

考研数学（数学二）模拟试卷744

选择题

1.设函数f(x)在x=0的某邻域内有定义，且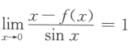(D)

A. f(0)=0

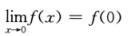B. C. 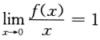D. 当x→0时，f(x)是x的高阶无穷小

解析：由题意，有，即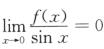

2.设f(x)=| t | t-x | dt，则（ ）．(D)

A. f’(0)存在，但f’(x)在x=0处不连续

B. f’(x)在x=0处连续，但f\\

C. f’(1)存在，但f’(x)在x=1处不连续

D. f’(x)在x=1处连续，但f\\

解析：当x≤0时，

f(x)=∫₀¹t(t—x)dt=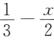

当0＜x≤1时，

f(x)=∫₀^xt(x-t)dt+∫_x¹t(t—x)dt

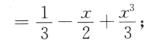
当x＞1时，

f(x)=∫₀¹ t(x—t)dt=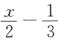

则

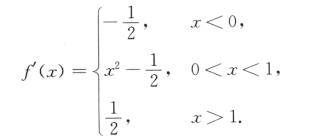
又

f’_–(0)=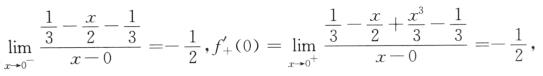

可知f’_–(0)=f’₊(0)，故f’(0)=-1/2．

又 f‘_–(1)=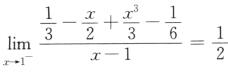，f’₊(1)=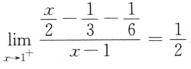

可知f’_–(1)=f’₊(1)，故f’(1)=1/2．

故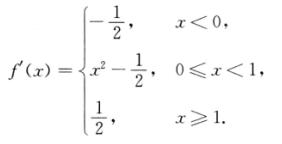

3.设函数f(x)可导，则任给a＜b，均有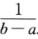∫_a^b-f(x)dx=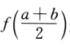(C)

A. 充分不必要条件

B. 必要不充分条件

C. 充要条件

D. 既不充分也不必要条件

解析：充分性．由于任给a，b，且a＜b，取a=c-t，b=c+t，c为任意值，t＞0，则有

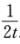∫_c-t^c+tf(x)dx=f(C)，

即 ∫_c-t^c+t f(x)dx=2t·f(C)．

上式两边对t求导，得 f(c+t)+f(c-t)=2f(C)．

两边继续对t求导，得 f’(c+t)-f’(c-t)=0．

令c=t＞0，有f’(2f)-f’(0)=0；令c=-t＜0，有f’(0)-f’(-2t)=0．

由于f’(0)是常数，故f’(2t)=f’(-2t)=f’(0)，为常数，即f(x)为一次多项式，故f(x)为直线．

必要性．设f(x)=dx+e，d，e为常数，则

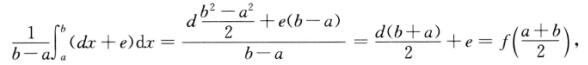
4.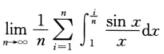(B)

A. 1—2cos 1

B. cos 1—1

C. 1—2sin 1

D. sin 1—1

解析：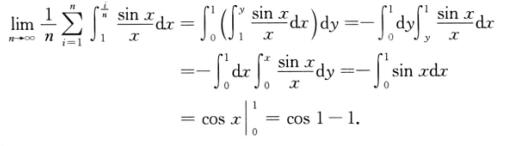

5.曲线r=本文档预览：3000字符，共15042字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载