考研数学一（高等数学）模拟试卷396

考研数学一（高等数学）模拟试卷396

选择题

1.若e^—x是f(x)的—个原函数，则(A)

A. —1/4

B. —1

C. 1/4

D. 1

解析：由于f(x)=(e^—x)’=—e^—x，所以f(1n x)=—e^{—1n x}=—1/x，从而

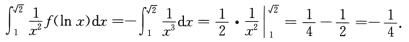
2.设g(x)=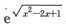，则( )．

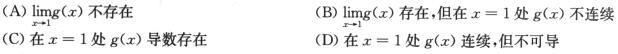(D)

A.

B.

C.

D.

解析：函数g(x)=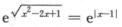的定义域是(—∞，+∞)，利用“初等函数在其定义区间

上是连续的”这—结论可得g(x)在x=1处连续，故排除选项A和B．

又因为

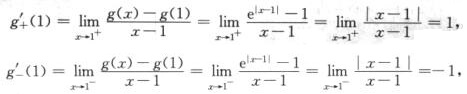
3.已知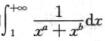(C)

A. α≤1

B. b≤1

C. α＞1

D. b＞1

解析：只需盯着x→+∞看，又由于α＞b＞0，因此原积分与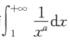

4.设f(x，y)有二阶连续偏导数，f(x，0)=2x+1，f’_y(1，y)=y+1—e^—y，f”_xy(x，y)=2x+y，则f(x，y)=( )．(C)

A. x²y+1/2xy²—e^—y—2x

B. xy²—1/2x²y—e^—y2—2x

C. x²y+1/2xy²+e^—y+2x

D. xy²+1/2x²y+e^—y+2x

解析：由f”_xy(x，y)=2x+y，得

f’_y(x，y)=x²+xy+g(y)．

由f’_y(1，y)=1+y+g(y)=y+1—e^—y得g(y)=—e^—y，故f’_y(x，y)=x²+xy—e^—y．则

f(x，y)=x²y+1/2xy²+e^—y+h(x)，

又f(x，0)=2x+1=1+h(x)，故h(x)=2x．所以f(x，y)=x²y+1/2xy²+e^—y+2x

5.设f(x)=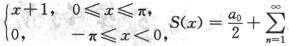(α_ncos nx+b_nsin nx)是f(x)以2π为周期的傅里叶级数，则=( )．

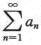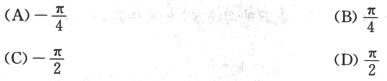(A)

A.

B.

C.

D.

解析：傅里叶系数α₀=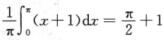，又由狄利克雷收敛定理，有

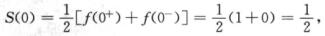
故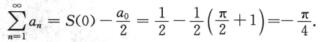

填空题

6.设f(x)在x=0处可导，f(0)=f’(0)=

4

解析：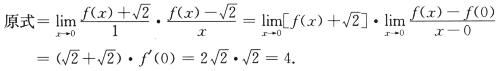

7.设存在0＜θ＜1，使得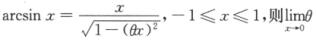

[*]

解析：

故

因为当x→0时，arcsin x=x+1/6x²+o(x³)，故(arcsin x+x)(arcsin x—x)～1/3 x⁴(x→0)，所以原式=本文档预览：3000字符，共8176字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载