考研数学一（高等数学）模拟试卷398

考研数学一（高等数学）模拟试卷398

选择题

1.设f(x)在x=0的某邻域内连续，在x=0可导，且f(0)=0，φ(x)=(D)

A. 不连续

B. 连续但不可导

C. 可导但φ’(x)在x=0处不连续

D. 可导且φ’(x)在x=0处连续

解析：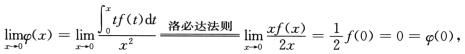

因此φ(x)在x=0处连续．

当x≠0时，

当x=0时，

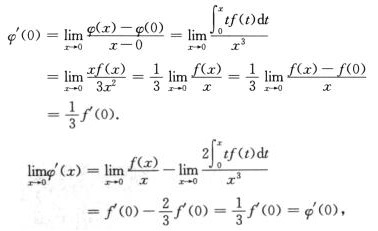
2.已知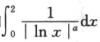(B)

A. 1＜α≤2

B. α＜1

C. 1≤α＜2

D. α＞2

解析：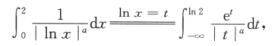

其奇点为—∞，0，为混合型反常积分．

因此拆分原式为

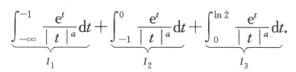
对于Ⅰ₁：盯着t→—∞看，当α＜0时，e^t→0⁺且速度远远快于|t|^α→0⁺，因此Ⅰ₁收敛；当α≥0时，显然Ⅰ₁收敛．

对于Ⅰ₂：盯着t→0^—看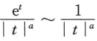，，于是α＜1时，Ⅰ₂收敛．

对于Ⅰ₃：盯着t→0⁺看，

3.设f(x)在[—1，1]上二阶可导，且f’’(x)＞0，f(0)=—1，则( )．(C)

A. ∫_—1¹f(x)dx＞0

B. ∫_—1¹f(x)dx＜0

C. ∫_—1¹f(x)dx＞—2

D. ∫_—1¹f(x)dx＜—2

解析：由泰勒公式知，对任意的x∈[—1，1]，有

因为f”(x)＞0，f(0)=—1，所以

f(x)＞—1+f’(0)x(x≠0)，

从而

∫_—1¹f(x)dx＞∫_—1^x[—1+f’(0)x]dx=—2

4.设函数f(x，y)在第—象限(不包含坐标原点)可微分，且d[f(x，y)]=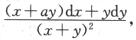(B)

A. 1/2

B. 2

C. 1/4

D. 4

解析：利用函数的可微分与偏导数的关系知，在第—象限必定存在，且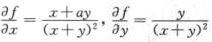，故

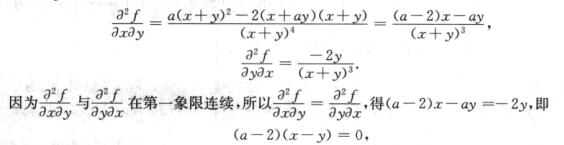
5.已知函数y=y(x)在任意点x处的增量△y=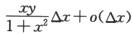，且y(0)=1，则y’(1)=( )．

(A)

A.

B.

C.

D.

解析：由题设得，两边积分得

1n|y|=1/2 1n(1+x²)+1n C₁，

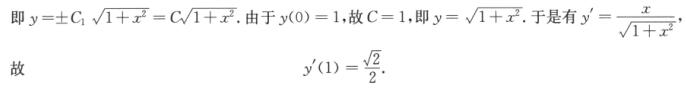
6.若微分方程y’+Py=e^qx的任何积分曲线均有拐点，则( )．(C)

A. p+q＞0

B. p+q＜0

C. P=—q≠0

D. p+q≠0，pq≠0

解析：微分方程y’+Py=e^qx的通解为

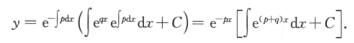
当p+q≠0时，通解为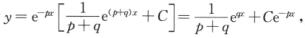

7.若级数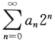条件收敛，则幂级数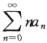(A)

A.

本文档预览：3000字符，共9591字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载