考研数学一（线性代数）模拟试卷171
选择题
1.若f(x)=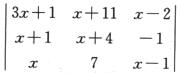
(B)
A. (1，7)
B. (—1，—1)
C. (0，0)
D. (—2，—2)
解析：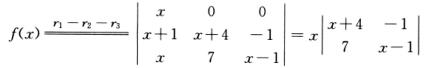
2.设A，B为3阶矩阵，且AB=
(C)
A. 互换矩阵A—1的第1，2行得矩阵B
B. 互换矩阵A—1的第1，2列得矩阵B—1
C. 互换矩阵A的第1，2行得矩阵B—1
D. 互换矩阵A的第1，2列得矩阵B—1
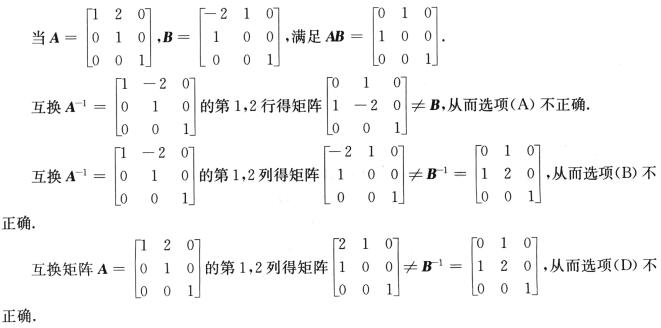
解析：由AB=
，故互换矩阵A的第1，2行得矩阵B—1，选项C正确．
现举例说明选项A，B，D不正确．
3.已知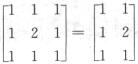
A，则A=( )．
(A)
A.
B.
C.
D.
解析：令α1=[1，1，1]T，α2=[1，2，1]T，观察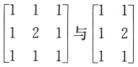
，可记为[α1，α2，α1]与[α1，α2]，故[α1，α2，α1]=[α1，α2]
4.下列矩阵中，不能相似对角化的是( )．
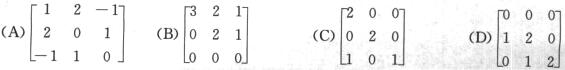(D)
A.
B.
C.
D.
解析：记四个选项中的矩阵依次为A，B，C，D.由于A为实对称矩阵，因此A可相似对角化．显然，B，C，D的特征值依次为3，2，0；2，2，1；0，2，2．由于B有三个不同的特征值，因此B可相似对角化．容易求得，r(2E—C)=1，r(2E—D)=2，故C的二重特征值2对应两个线性无关的特征向量，而D的二重特征值2仅对应—个线性无关的特征向量．因此，C可相似对角化，D不可相似对角化．
5.设A为n阶可逆矩阵，α为n维列向量．记分块矩阵Q=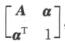
(C)
A. αTAα≠1
B. αTAα≠—1
C. αTA—1α≠1
D. αTA—1α≠—1
解析：令P=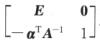
则
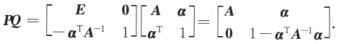
6.设A为m×n矩阵，e=[1，1，…，1]T．若方程组Ay=e有解，则对于(Ⅰ)ATx=0与(Ⅱ)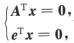
(D)
A. (Ⅰ)的解都是(Ⅱ)的解，但(Ⅱ)的解未必是(Ⅰ)的解
B. (Ⅱ)的解都是(Ⅰ)的解，但(Ⅰ)的解未必是(Ⅱ)的解
C. (Ⅰ)的解不是(Ⅱ)的解，且(Ⅱ)的解也不是(Ⅰ)的解
D. (Ⅰ)的解都是(Ⅱ)的解，且(Ⅱ)的解也都是(Ⅰ)的解
解析：显然方程组(Ⅱ)的解都是方程(Ⅰ)的解．由Ay=e有解，知rA=r([A,e])，于是
r(AT)=r([A，e]T)=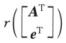
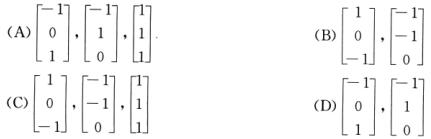
7.设向量空间V满足x1+x2+x3=0，—∞＜xi＜+∞，i=1，2，3，则V的—个基为( )．
(D)
A.
B.
C.
D.
解析：由x1+x2+x3=0，解得
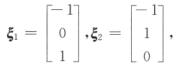
8.设A是3阶矩阵，有特征值λ1=0,λ2=1，λ3=—1，对应的特征向量分别是ξ1，
本文档预览：3000字符，共22014字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
