考研数学一（随机变量及其分布、多维随机变量及其分布）模拟试卷1

考研数学一（随机变量及其分布、多维随机变量及其分布）模拟试卷1

选择题

1.设随机变量X的密度函数为f(x)，且f(x)为偶函数，X的分布函数为F(x)，则对任意实数a，有( )．(B)

A. F(-a)=1-∫₀^af(x)dx

B. F(-a)=1／2-∫₀^af(x)dx

C. F(-a)=F(a)

D. F(-a)=2F(a)-1

解析：F(-a)=∫_-∞^-af(x)dx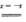

2.设随机变量X的分布函数为F(x)，则下列函数中可作为某随机变量的分布函数的是( )．(D)

A. F(x²)

B. F(-x)

C. 1-F(x)

D. F(2x-1)

解析：函数φ(x)可作为某一随机变量的分布函数的充分必要条件是：

(1)0≤φ(x)≤1； (2)φ(x)单调不减；

(3)φ(x)右连续； (4)φ(-∞)=0，φ(+∞)=1．

显然只有F(2x-1)满足条件，选D．

3.设随机变量X，Y相互独立，它们的分布函数为F_X(x)，F_Y(y)，则Z=min{X，Y}的分布函数为( )．

C

解析：F_Z(z)=P(Z≤z)=P(min{X，Y}≤z)=1-P(min{X，Y}＞z)

=1-P(X＞z，Y＞z)=1-P(X＞z)P(Y＞z)

=1-[1-P(X≤z)][1-P(Y≤z)]

=1-[1-F_X(z)][1-F_Y(z)]，选C．

4.设随机变量X与Y相互独立且都服从参数为λ的指数分布，则下列随机变量中服从参数为2λ的指数分布的是( )．

D

解析：由于X～E(λ)，所以密度函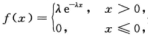数为分布函数为

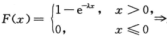E(X)=1／λ，D(X)=1／λ²，因为E(X+Y)=2／λ，E(X-Y)=0，

而max{X，Y}的分布函数是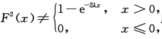所以A，B，C项都不对，选D．

事实上，min{X，Y)的分布函数为P(min{X，Y)≤x)=1-P(min{X，Y)＞x)=1-P(X＞x，Y＞x)

=1-P(X＞x)P(Y＞x)=1-[1-F(x)]²=

5.若(X，Y)服从二维正态分布，则①X，Y一定相互独立；②若ρ_XY=0，则X，Y一定相互独立；③X和Y都服从一维正态分布；④X，Y的任一线性组合服从一维正态分布．上述几种说法中正确的是( )．(B)

A. ①②③

B. ②③④

C. ①③④

D. ①②④

解析：因为(X，Y)服从二维正态分布，所以X，Y都服从一维正态分布，aX+bY服从一维正态分布，且X，Y独立与不相关等价，选B．

6.设随机变量X，Y相互独立，且X～N(0，1／2)，Y～N(1，1／2)，则与Z=Y-X同分布的随机变量是( )．(B)

A. X-Y

B. X+Y

C. X-2Y

D. Y-2X

解析：Z=Y-X～N(1，1)，因为X-Y～N(-1，1)，X+Y～N(1，1)．

X-2Y～N(-2，5／2)，Y=2X～N(1，5／2)，所以选B．

填空题

7.设一次试验成功的概率为p，进行100次独立重复试验，当p=________时，成功次数的标准差最大，其最大值为________．

1／2，5．

解析：设成功的次数为X，则X～B(100，p)．

D(X)=100p(1-p)，标准差为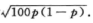

8.设随机变量X的概率密度为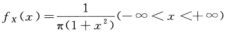

[*]

解析：F_Y(y)=P(Y≤y)=P(X²≤y)．

当y≤0时，F_Y(y)=0；

当y＞0时，F_Y(y)=P(X²≤y)=P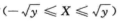

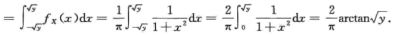
于是故本文档预览：3000字符，共8755字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载