
考研数学一(大数定律和中心极限定理、数理统计的基本概念、参数估计、假设检验)模拟试卷1
选择题
1.设X1,X2,…,Xn是来自正态总体X~N(μ,σ2)的简单随机样本,记
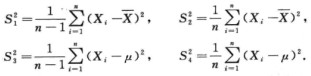 (D)
(D)
A. 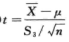 B.
B. 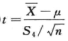 C.
C. 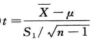 D.
D. 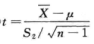 解析:
解析: ,即
,即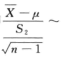
2.设总体X~N(0,σ2),X1,X2,…,Xn为总体X的简单随机样本,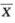 (A)
(A)
A. 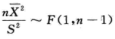 B.
B. 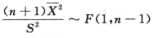 C.
C.  D.
D.  解析:由
解析:由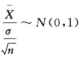 得
得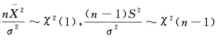 且
且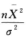 与
与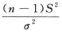 相互独立.
相互独立.
于是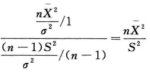
3.从正态总体X~N(0,σ2)中抽取简单随机样本X1,X2,…,Xn,则可作为参数σ2的无偏估计量的是( ).(A)
A.  B.
B.  C.
C. 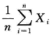 D.
D. 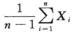 解析:因为
解析:因为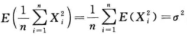 ,所以
,所以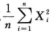
填空题
4.设随机变量X,Y不相关,X~U(-3,3),Y的密度为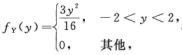
2/5.
解析:E(X)=0, D(X)=3, E(Y)=0, D(Y)=12/5.
则E(X-Y)=0,D(X-Y)=D(x)+D(y)-2Cov(X,Y)=27/5,所以
P(|X-Y|<3)=P(|(X-Y)-E(X-Y)|<3)≥1-D(X-Y)/9=2/5.
5.设随机变量X1,X2,…,X10相互独立且Xi~P(i)(i=1,2,…,10),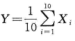
34/45.
解析:(2)由Xi~P(i)得E(Xi)=i,D(Xi)=i(i=1,2,…,10),

