
考研数学一(矩阵的特征值和特征向量)模拟试卷17
选择题
1.设三阶矩阵A的特征值为-1,1,2,其对应的特征向量为α1,α2,α3,令P=(3α2,-α3,2α1),则P-1AP等于( ).(C)
A.  B.
B. 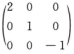 C.
C. 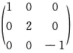 D.
D.  解析:显然3α2-α3,2α1也是特征值1,2,-1的特征向量,所以
解析:显然3α2-α3,2α1也是特征值1,2,-1的特征向量,所以
2.设A,B为n阶矩阵,且A,B的特征值相同,则( ).(D)
A. A,B相似于同一个对角矩阵
B. 存在正交阵Q,使得QTAQ=B
C. r(A)=r(B)
D. 以上都不对
解析:令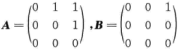
3.与矩阵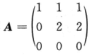 (D)
(D)
A.  B.
B.  C.
C.  D.
D. 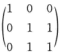 解析:A的特征值为1,2,0,因为特征值都是单值,所以A可以对角化,又因为给定的四个矩阵中只有选项D中的矩阵特征值与A相同且可以对角化,所以选D.
解析:A的特征值为1,2,0,因为特征值都是单值,所以A可以对角化,又因为给定的四个矩阵中只有选项D中的矩阵特征值与A相同且可以对角化,所以选D.
4.设A,B为n阶可逆矩阵,则( ).(D)
A. 存在可逆矩阵P,使得P-1AP=B
B. 存在正交矩阵Q,使得QTAQ=B
C. A,B与同一个对角矩阵相似
D. 存在可逆矩阵P,Q,使得PAQ=B
解析:因为A,B都是可逆矩阵,所以A,B等价,即存在可逆矩阵P,Q,使得PAQ=B,选D.
填空题
5.设
-2.
解析:因为|A*|=|A|2=4,且|A|>0,所以|A|=2,又AA*=|A|E=2E,所以A-1=1/2A*,从而A-1的特征值为-1/2,-1,1,根据逆矩阵之间特征值的倒数关系,则A的特征值为-2,-1,1,于是a11+a22+a33=-2-1+1=-2.
6.设λ1,λ2,λ3是三阶矩阵A的三个不同特征值,α1,α2,α1分别是属于特征值λ1,λ2,λ3的特征向量,若α1,A(α1+α2),A2(α1+α2+α3)线性无关,则λ1,λ2,λ3满足________.
λ1λ32≠0.
解析:令x1α1+x2A(α1+α2)+x3A2(α1+α2+α3)=0,即
(x1+λ1x2+λ12x3)α1+(λ2x2+λ22x3)α2+λ32x3α3=0,
则有x1+λ1x2+λ12x3=0, λ2x2+λ22
本文档预览:3000字符,共11104字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载