考研数学一（行列式、矩阵）模拟试卷7

考研数学一（行列式、矩阵）模拟试卷7

选择题

1.设α₁，α₂，α₃，β₁，β₂都是四维列向量，且｜A｜=｜α₁，α₂，α₃，β₁｜=m，｜B｜=｜α₁，α₂，β₂，α₃｜=n，则｜α₃，α₂，α₁，β₁+β₂｜为( )．(D)

A. m+n

B. m-n

C. -(m+n)

D. n-m

解析：｜α₃，α₂，α₁，β₁+β₂｜=｜α₃，α₂，α₁，β₁｜+｜α₃，α₂，α₁，β₂｜

=-｜α₁，α₂，α₃，β₁｜-｜α₁，α₂，α₃，β₂｜

=-｜α₁，α₂，α₃，β₁｜+｜α₁，α₂，β₂，α₃｜=n-m，

选D．

2.设A为三阶矩阵，｜A｜=4，则｜-2A^-1+A^*｜=( )．(A)

A. 2

B. -2

C. 4

D. -4

解析：由A^*=｜A｜A^-1=4A^-1得｜-2A^-1+A^*｜=｜2A^-1｜=8｜A^-1｜=8／｜A｜=2，选A．

3.设A为m阶矩阵，B为n阶矩阵，则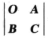(B)

A. ｜A｜·｜B｜

B. (-1)^mn｜A｜·｜B｜

C. ｜A｜·｜C｜

D. ｜B｜·｜C｜

解析：由行列式的性质得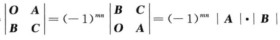

4.设A是m×n矩阵，B是n×m矩阵，则( )．(B)

A. 当m＞n时，必有｜AB｜≠0

B. 当m＞n时，必有｜AB｜=0

C. 当n＞m时，必有｜AB｜≠0

D. 当n＞m时，必有｜AB｜=0

解析：AB为m阶矩阵，因为r(A)≤min{m，n}，r(B)≤min{m，n}，且r(AB)≤min{r(A)，r(B)}，所以r(AB)≤min{m，n}，故当m＞n时，r(AB)≤n＜m，于是｜AB｜=0，选B．

5.设A，B都是n阶可逆矩阵，则( )．(B)

A. (A+B)^*=A^*+B^*

B. (AB)^*=B^*A^*

C. (A-B)^*=A^*-B^*

D. (A+B)^*一定可逆

解析：因为(AB)^*=｜AB｜(AB)^-1=｜A｜｜B｜B^-1A^-1=｜B｜B^-1·｜A｜A^-1=B^*A^*，所以选B．

6.设A为n阶矩阵，A²=A，则下列成立的是( )．(D)

A. A=O

B. A=E

C. 若A不可逆，则A=O

D. 若A可逆，则A=E

解析：因为A²=A，所以A(E-A)=O，由矩阵秩的性质得r(A)+r(E-A)=n，若A可逆，则r(A)=n，所以r(E-A)=0，A=E，选D．

7.设A为4×3矩阵，B≠O，下列正确的是( )．(D)

A. 若AB=O且r(A)=1，则r(B)=2

B. 若AB=O且r(A)-1，则r(B)=1

C. 若AB=O且r(A)=2，则r(B)=2

D. 若AB=O且r(A)=2，则r(B)=1

解析：由AB=O得r(A)+r(B)≤3，若r(A)=1，则r(B)≤2；

又由B≠O得r(B)≥1，故1≤r(B)≤2，A、B错误；

若r(A)=2，则r(B)≤1，又r(B)≥1，所以r(B)=1，选D．

8.设(C)

A. -8

B. -24

C. -12

D. 12

解析：由题意得，｜A｜=-24，令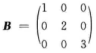，C=(4)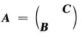，，A^{-1本文档预览：3000字符，共8540字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载}