考研数学二（微分中值定理及其应用）模拟试卷12
选择题
1.设函数y＝f(x)具有二阶导数，且f’(x)＞0，f’’(x)＞0，△x为自变量x在点x0处的增量， △y与dy分别为f(x)在点x0处相应的增量与微分，若△x＞0，则________．(A)
A. 0＜dy＜△y
B. 0＜△y＜dy
C. △y＜dy＜0
D. dy＜△y＜0
解析：当△x＞0时， △y＝f(x0＋△x)－f(x0)－f’(ξ)△x，其中x0＜ξ＜x0＋△x，由f’(x)＞0，f’’(x)＞0，得0＜f’(x0)＜f’(ξ)，所以0＜dy＝f’(x0)△x＜f’(ξ)△x＝△y.
故应选A.
2.设函数y＝f(x)在(0，＋∞)内有界且可导，则
(B)
A.
B.
C.
D.
解析：对y＝f(x)在区间[a，x]上使用拉格朗口中值定理，得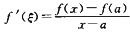
其中ξ介于a与x之间.
因为f(x)在[a，x]
(0，＋∞)上有界，所以f(x)－f(a)有界，
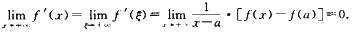
3.设f(x)处处可导，则________．
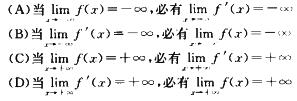(D)
A.
B.
C.
D.
解析：由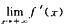
4.以下四个命题中，正确的是________．(C)
A. 若f’(x)在(0，1)内连续，则f(x)在(0，1)内有界
B. 若f(x)在(0，1)内连续，则f(x)在(0，1)内有界
C. 若f’(x)在(0，1)内有界，则f(x)在(0，1)内有界.
D. 若f(x)在(0，1)内有界，则f’(x)在(0，1)内有界
解析：通过举反例用排除法找到正确答案即可.
设f(x)＝1／x，则f(x)及f’(x)＝－1／x2均在(0，1)内连续，但f(x)在(0，1)内无界，排除A、B；又f(x)＝
在(0，1)内有界，但f’(x)＝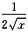
5.设函数f(x)在闭区间[a，b]上有定义.在开区间(a，b)内可导，则________．(B)
A. 当f(a)f(b)＜0时，存在∈(a，b)，使f(ξ)＝0
B. 对任何∈(a，b)，有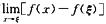
C. 当f(a)＝f(b)时，存在ξ∈(a，b)，使f’(ξ)＝0
D. 存在ξ∈(a，b)，使f(b)－f(a)＝f’(ξ)(b－a)
解析：选项A，C，D均不确定 ，因已知条件中f(x)仅在[a，b]上有定义，不能保证f(x) 在[a，b]上的连续性.
对于选项B:不妨设ξ＜x，则f(x)在[ξ，x](a，b)上连续，在(ξ，x)内可导，由拉格朗日中，值定理知至少存在一点t∈(ξ，x)，使f(x)－f(ξ)＝ f’(t)(x－ξ)，从而
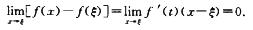
6.设在[0，1]上，f’’(x)＞0，则f’(0)，f’(1)，f(1)－f(0)或f(0)－ f(1)的大小顺序是________．(B)
A. f’(1)＞f’(0)＞f(1)－f(0)
B. f’(1)＞f(1)－f(0)＞f’(0)
C. f(1)－f(0)＞f’(1)＞f’(0)
D. f’(1)＞f(0)－f(1)＞f’(0)
解析：因为f’’(x)＞0，所以 f’(x)在[0，1]上单调递增.故f’(1)＞f’(0)，而由拉格朗日中值定理知f(1)－f(0)＝f’(ξ)(1－0)，其中ξ介于0与1之间，则f’(0)＜f’(ξ)＜f’(1).
故应选B.
解答题
7.罗尔定理对y＝ lnsinx在[π／6，5π／6]上的正确性.
y＝lnsinx的定义域为{x|2nπ＜x＜(2n＋1)π，n＝0，±1，±2，…}
因为初等函数在定义区间内连续，所以该函数在[π／6，5π／6]上连续；
又y’＝cotx在(π／6，5π／6)内处处存在，并且f(π／6)＝f(5π／6)＝－ln2，可知函数在[π／6，5π／6]上满足罗尔定理条件.
由y’＝cotx＝0在(π／6，5π／6)内显然有解x＝π／2，取ξ＝π／2，则f’(ξ)＝0.
解析：本文档预览：3000字符，共11337字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
