考研数学一（微分中值定理及其应用）模拟试卷11

考研数学一（微分中值定理及其应用）模拟试卷11

选择题

1.当x＞0时，曲线y＝ xsin(1／x)________．(A)

A. 有且仅有水平渐近线

B. 有且仅有铅直渐近线

C. 既有水平渐近线，也有铅直渐近线

D. 既无水平渐近线，也无铅直渐近线

解析：因为

2.曲线y＝1／x＋ln(1＋e^x)渐近线的条数为________．(D)

A. 0

B. 1

C. 2

D. 3

解析：只有闻断点x＝0，由于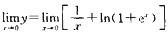＝∞，故x＝0为垂直渐近线.又＝0＋ln1＝0，故x→－∞时有水平渐近线y＝0.

又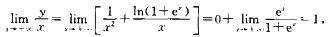

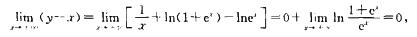
3.曲线y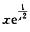＝ (D)

A. 仅有水平渐近线

B. 仅有铅直渐近线

C. 既有铅直又有水平渐近线

D. 既有铅直又有斜渐近线

解析：当x→∞时，极限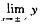均不存在，故不存在水平渐近线:又因为

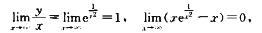
所以有斜渐近线y＝x.

另外，在x＝0处y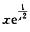＝无定义，且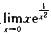＝∞，可见x＝0为铅直渐近线，所以曲线y＝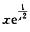

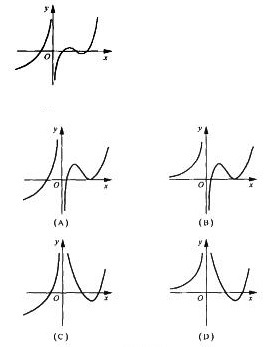
4.设函数f(x)在定义城内可导，y＝ f(x)的图形如图所示，则导函数y＝f’(x)的图形如选项中的________.

(D)

A.

B.

C.

D.

解析：根据y＝f(x)图形知:当 x＜0时，f(x)单调递增，故f’(x)＞0，排除A，C.当x＞0时，f(x)图形由凸→凹，则f’’(x)由－→＋，即f’(x)由单减→单增，排除@B@.

故应选D.

填空题

5.曲线y＝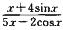

y＝1／5

解析：因为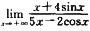

6.曲线y＝ xln(e＋1／x)(x＞0)的渐近线方程为______.

y＝x＋1／e

解析：设y＝ax＋b为曲线的渐近线，则

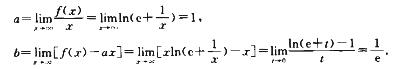
7.曲线y＝(2x－1)e^1／x的斜浙近线方程为________．

y＝2x＋1

解析：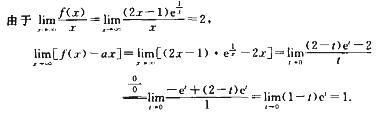

解答题

8.设y＝f(x)是方程y’’－2y’＋4y＝0的一个解，若f(x₀)＞0，且f’(x₀)＝0，试判定它是否是f(x)的极值点?如果x₀为f(x)的极值点，是极大值点，还是极小值点?

由于 y＝f(x)为y’’－2y’＋4y＝0的解，从而f’’(x)－2f’(x)＋4f(x)＝0，特别，当f(x₀)＞0，f’(x₀0时，上述方程可以化为

f’’(x₀)＋4f(x₀)＝0，即f’’(x₀)＝－4f(x₀)＜0，

由极值的第二充分条件可以得知，x₀为f(x)的极值点，且为极大值点，即f(x)在x₀点取得极大值.

解析：

9.设函数y＝ y(x)由方程2y³－2y²＋2xy－x²＝1所确定，试求y＝y(x)的驻点，并判，定它是否为极值点.

对原方程两边关于x求导可得

3y²y’－2yy’＋xy’＋y－x＝0，①<

本文档预览：3000字符，共9881字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载