考研数学一（微分中值定理及其应用）模拟试卷10
选择题
1.当a取下列哪个值时，函数f(x)＝2x3－9x2＋12x－a恰有两个不同的零点________.(B)
A. 2
B. 4
C. 6
D. 8
解析：f’(x)＝6x2－18x＋12－6(x－1)(x－2)，从而f(x)可能的极值点为x＝1，x＝2，且f(1)＝5－a，f(2)＝4－a，可见当a＝4时，函数f(x)恰好有两个零点。
故应选B.
2.设常数k＞0，函数f(x)＝lnx－x／e＋k在(0，＋∞)内零点个数为________．(B)
A. 3
B. 2
C. 1
D. 0
解析：因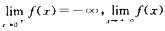
3.在区间(－∞，＋∞)内，方程|x|1／4＋|x|1／2－cosx＝0.(C)
A. 无实根
B. 有且仅有一个实根
C. 有且仅有二个实根
D. 有无穷多个实根
解析：当x∈[0，＋∞)时，令 f(x)＝x1／4＋x1／2－cosx，显然，f(0)＝－1＜0，f(1)＝2－cos1＞0，由零点定理知在(0，1)内至少有一个f(x)＝0的根，易知f’(x)＝x－3／4 ／4＋x1／2／2＋sinx，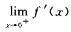
4.曲线y＝x3－x2________．(C)
A. 没有拐点
B. 有两个拐点
C. 有一个拐点
D. 有三个拐点
解析：y’＝3x2－2x，y’’＝6x－2＝0，解得x＝1／3，且y’’在x＝1／3的左、右两侧改变符号，所以x＝1／3为曲线y＝x3－x2的拐点.
故应选C.
5.曲线y＝(x－1)2＝(x－3)2的拐点个数为________．(C)
A. 0
B. 1
C. 2
D. 3
解析：y’＝2(x－1)(x－3)2＋2(x－1)2(x－3)，y’’＝4(3x2－12x＋11)＝0.
解得y’’＝0有两个根，且根两侧二阶导数符号变号.
故应选C.
6.设f(x)＝|x(1－x)|，则________．(C)
A. x ＝0是f(x)的极值点，但(0，0)不是曲线y＝f’(x)的拐点
B. x＝0不是f(x)的极值点，但(0，0)是曲线y＝ f(x)的拐点
C. x ＝0是f(x)的极值点，且(0，0)是曲线y＝ f(x)的拐点
D. x＝0不是f(x)的极值点，且(0，0)也不是曲线y＝ f(x)的拐点
解析：f(x)在x＝0附近的表达式为
f(x)＝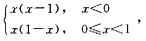
从而f’(x)＝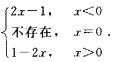
由于f’(0)不存在，且f’(x)在x＝0左右两边符号改变，故x＝0是f(x)的极值点又f’’(0)＝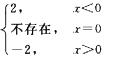
7.设f’(x0)＝f’’(x0)＝0，f’’’(x0)＞0，则下列选项正确的是________．(D)
A. f’(x0)是f’(x)的极大值
B. f(x0)是(x)的极大值
C. f(x0)是f(x)的极小值
D. (x0，f(x0))是曲线y＝ f(x)的拐点
解析：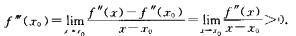
8.设函数f(x)满足关系式f’’(x)＋[f’(x)]2＝x，且f’(0)＝0，则(C)
A. f(0)是 f(x)的极大值
B. f(0)是 f(x)的极小值
C. 点(0，f(0))是曲线y＝ f(x)的拐点
D. f(0)不是f(x)的极值，点(0，f(0))也不是曲线y＝ f(x)的拐点
解析：在关系式中令x＝0得f’’(0)＝0，对f’’(x)＝x－[f’(x)]2两边关于x求导得
f’’’(x)＝1－2f’(x)f’’(x).
令x＝0，f’’(0)＝1＞0，所以(0，f(0))是曲线y＝ f(x)拐点．
故应选C.
9.函数y＝|1＋sinx|在区间(π，2π)内的图形是________．(A)
A. 凹的
B. 凸的
C. 既是凹的又是凸的
D. 为直线
解析：当x∈(π，2π)时，－1≤sinx≤0，从而0≤1＋sinx≤1，所以
y＝|1＋sinx|＝1＋sinx，y’＝cosx， y’’＝－ sinx＞0，
从而函数y＝ |1＋sinx|在(π，2π)内为凹的.
故应选A.
10.设f(x)＝ xsinx＋cosx，下列命题中正确的是________
本文档预览：3000字符，共9284字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
