
考研数学二(微分中值定理及其应用)模拟试卷13
选择题
1.设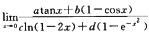 (D)
(D)
A. b=4d
B. b=-4d
C. a=4c
D. a=-4c
解析: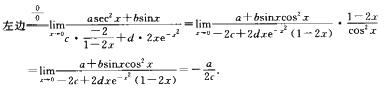
2.设x→0时,etanx-ex与xn是同阶无穷小,则n为________.(C)
A. 1
B. 2
C. 3
D. 4
解析: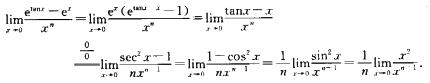
填空题
3.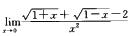
-1/4
解析: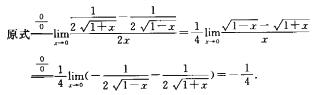
4.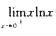
0
解析: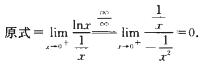
5.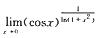
[*]
解析: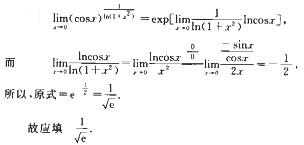
6.当x→0时,a(x)=kx2与β(x)= 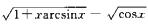
3/4
解析:由题设,

解答题
7.设函数f(x)在[a,b]上连续,在(a,b)内可导,且f’(x)≠0.试证:存在ξ,η∈(a,b),使得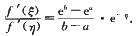
令g(x)=ex,则g(x)与f(x)在[a,b]上满足柯西中值定理条件,故由柯西中值定理,存在η∈(a,b),使得
[*]
又f(x)在[a,b]上满足拉格朗日中值定理条件,故存在ξ∈(a,b),使
[*]
由题设f’(x)≠0知,f’(η)≠0,从而[*]
解析:
8.试证:sinl = coslnξ, 1<ξ<e.
设F(x)=sinlnx,G(x)=lnx,则F(x),G(x)在[1,e]上满足柯西中值定理条件.由于
F(1)= sin ln1=0,F(e) = sinlne= sin1,
G(1)=ln1=0,G(e)=lne=1,
F’(x)=coslnx.(1/x),G’(x)=1/x,
故由柯西中值定理存在ξ∈(1,e),使得
[*]
解析:
9.计算: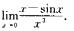
[*]
解析:
10.计算: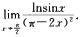
[*]
解析:
11.计算: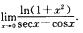
[*]
解析:
12.计算: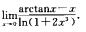
[*]
解析:
13.求
[*]
解析:
14.求极限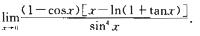
[*]
解析:
15.求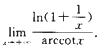
[*]
解析:
16.求
[*]
本文档预览:3000字符,共4620字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载
