
考研数学二(微分中值定理及其应用)模拟试卷14
选择题
1.设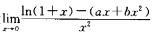 (A)
(A)
A. a=l,b=-2/5
B. a=0,b=-2
C. a=0,b=-5/2
D. a=1,b=-2
解析: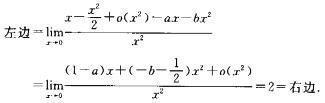
2.设当x→0时,ex-(ax2+bx+1)是比x2高阶的无穷小,则________.(A)
A. a=1/2,b=1
B. a=1,b=1
C. a=-1/2,b=1
D. a=-1,b=1
解析:由ex=1+x+x2/2!+o(x2)知ex-(ax2+bx+1)=(1-b)x+(1/2-a)x2+o(x2).
所以必有a=1/2,b=1.
3.设f(x)在(-∞,+∞)内可导,且对任意到的x1,x2,当x1>x2时,都有f(x1)>f(x2),则________.(D)
A. 对任意x,f’(x)>0
B. 对任意x,f’(-x)≤0
C. 函数f(-x)单调增加
D. 函数-f(-x)单调增加
解析:当x1>x2时,-x1<-x2,则f(-x1)<f(-x2),从而-f(-x2)>-f(-x2),即-f(-x)单调增加.
故应选D.
4.设f(x)、g(x)是恒大于零的可导函数,且f’(x)g(x)-f(x)g’(x)<0,则当a<x<b时,有________.(A)
A. f(x)g(b)> f(b)g(x)
B. f(x)g(a)>f(a)g(x)
C. f(x)g(x)> f(b)g(b)
D. f(x)g(x)> f(a)g(a)
解析:由
5.设在[0,1]上,f’’(x)≤0,则f’(0),f’(1),f(1)-f(0)或f(0)-f(1)的大小顺序是(B)
A. f’(1)≤f’(0)≤f(1)-f(0)
B. f’(1)≤f(1)-f(0)≤f’(0)
C. f(1)-f(0)≤f’(1)≤f’(0)
D. f’(1)≤f(0)-f(1)≤f’(0)
解析:因为f’’(x)≤0,所以f’(x)在[0,1]上单调不增,故f’(1)≤f’(0),而由拉格朗日中值定理,f(1)4f(0)=f’(ξ)(1-0),其中ξ介于0,1之间,则f’(1)≤f’(ξ)≤f’(0).
故应选B.
6.已知函数f(x)在区间(1-δ,1+δ)内具有二阶导数,f’(x)严格单调减少,且f(1)=f’(1)=1,则________.(A)
A. 在(1-δ,1)和(1,1+δ)内均有f(x)<x
B. 在(1-δ,1)和(1,1+δ)内均有f(x)>x
C. 在(1-δ,1)内,f(x)<x,在(1,1+δ)内,f(x)>x
D. 在(1-δ,1)内,f(x)>x,在(1,1+δ)内,f(x)<x
解析:设F(x)=f(x)-x.则 F(1)=f(1)-1=0.
F’(x)=f’(x)-1,F’(1)=f’(1)-1=0.
F’’(x)=f’’(x).由f’(x)在(1-δ,1+δ)内严格单调减少知F’’(x)<0,从而F’(x)在(1-δ, 1+δ)内单调减少,即x∈(1-δ,1)时,F(x)>F(1)=0,x∈(1,1+δ)时,F (x)<F’(1)=0.
当x∈(1-δ,1)时,由F’(x)>0知F(x)单增,即F(x)<F(1)=0,也即f(x)<x;
当x∈(1,1+δ)时,由F’(x)<0知F(x)单减,即F(x)<F(1)=0,也即f(x)<x.
故应选A.
7.若f(-x)=f(x) (-∞<x<+∞),在(-∞,0)内f’(x)>0且f’’(x)<0,则在(0,+∞)内有________.(C)
A. f’(x)>0,f’’(x)<0
B. f’(x)>0.f’’(x)>0
C. f’(x)<0,f’’(x)<0
D. f’(x)<0,f’’(x)>0
解析:由f(-x)=f(x)知,f(x)在(-∞,+∞)内为偶函数,f(x)的图象关于y轴对称,在(-∞,0)内,f’(x)>0说明f(x)为单调单增,f’’(x)<0说明f(x)为凸的,故f(x)在(0,+∞)内为单调递减凸函数,从而x∈(0,+∞)时,f’(x)<0,f’’(x)<0.
故应选C.
填空题
8.若f(x)=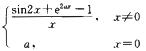
-2
解析:若f(x)在(-∞,+∞)上连续,则f(x)必在x=0处连续,即 = f(0)=a.而
= f(0)=a.而
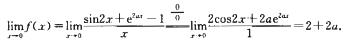
9.知f(x)= 本文档预览:3000字符,共8358字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载