
考研数学二(选择题)模拟试卷212
选择题
1.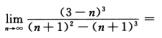 (D)
(D)
A. ∞.
B. 0.
C. -1.
D. 1.
解析:
2.下列命题中正确的是(D)
A. 若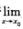 f(x)≥
f(x)≥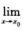 B. 若存在δ>0使得当0< |x-x0|<δ时有f(x)>g(x)且
B. 若存在δ>0使得当0< |x-x0|<δ时有f(x)>g(x)且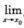 f(x)=A0,
f(x)=A0,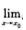 C. 若存在δ>0,当0<|x-x0|<δ时f(x)>g(x)→
C. 若存在δ>0,当0<|x-x0|<δ时f(x)>g(x)→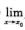 f(x)≥
f(x)≥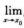 D. 若
D. 若 f(x)>
f(x)>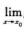 解析:D正确.D正是极限的不等式性质中所述的结论.A的错误在于由
解析:D正确.D正是极限的不等式性质中所述的结论.A的错误在于由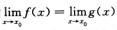
3.以下函数f(g(x))以x=0为第二类间断点的是(D)
A. f(u)=ln(1+u2),g(x)=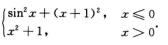 B. f(u)=
B. f(u)=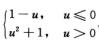 C. f(u)=
C. f(u)=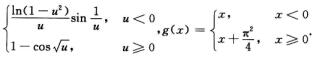 D. f(u)=
D. f(u)=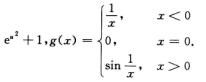 解析:易知A,B中f(u)在(-∞,+∞)连续,g(x)在(-∞,+∞)连续
解析:易知A,B中f(u)在(-∞,+∞)连续,g(x)在(-∞,+∞)连续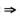 复合函数f(g(x))在(-∞,+∞)连续.因此只须在C,D中选择.
复合函数f(g(x))在(-∞,+∞)连续.因此只须在C,D中选择.
考察C
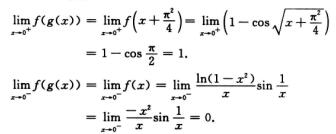
4.设f(0)=0,f′(x)在[0,+∞)为严格单调增函数,则函数g(x)=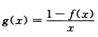 (D)
(D)
A. 有界函数.
B. 有极值.
C. 单调增函数.
D. 单调减函数.
解析:
因为f(0)=0,所以由中值定理知f(x)=xf′(ξ),其中0<ξ<x.所以
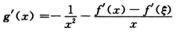
而f′(x)在(0,+∞)为严格单调增函数,所以g′(x)<<0,函数g(x)=
5.设f(x)在(1-δ,1+δ)内存在导数,f′(x)单调减少,且f(1)=f′(1)=1,则(A)
A. 在(1-δ,1)和(1,1+δ)内均有f(x)<x.
B. 在(1-δ,1)和(1,1+δ)内均有f(x)>x
C. 在(1-δ,1)内有f(x)<x,在(1,1+δ)内有f(x)>x.
D. 在(1-δ,1)内有f(x)>x,在(1,1+δ)内有f(x)<x.
解析:为考察f(x)与x之间的关系,设F(x)=f(x)-x,则F(x)=f′(x)-1,F′(x)在(1-δ,1+δ)单调减少,F′(1)=0,F(1)=0.
当x∈(1-δ,1)时,F′(x)>F′(1)=0,因此F(x)在(1-δ,1]内单调递增,F(x)<F(1)=0,即在(1-δ,1)内F(x)<0.
当x∈(1,1+δ)时,F′(x)<F′(1)=0,因此F(x)在[1,1+δ)内单调递减,F(x)<F(1)=0,即在(1,1+δ)内F(x)<0.因此,选A.
6.I=∫01x4