考研数学二（填空题）模拟试卷197

考研数学二（填空题）模拟试卷197

填空题

1.计算极限

1

解析：由洛必达法则和变限积分函数求导公式，可得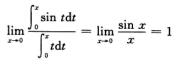

2.

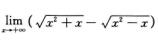
1

解析：分子有理化，

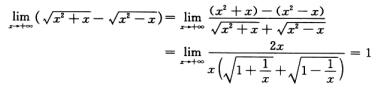
3.设a，b为常数，且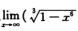

-1，0

解析：由泰勒展开，当x→∞时，

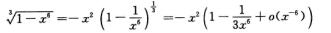
4.设f(x)是以3为周期的可导函数且是偶函数，f′(-2)=-1，则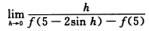

-1/2

解析：f′(0)以3为周期且是奇函数：

f′(5)=f′(2)=-f′(-2)

现按导数定义求此极限．

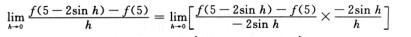
5.设f(x)=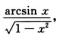

[*]

解析：f(x)=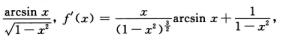

(1-x²)f′(x)-xf(x)-1=0

[(1-x²)f′(x)-xf(x)-1]⁽ⁿ⁾=0

[(1-x²)f′(x)]⁽ⁿ⁾-[xf(x)]⁽ⁿ⁾=0

(1-x²)f⁽ⁿ⁺¹⁾(x)-(2n+1)xf⁽ⁿ⁾(x)-n²f^(n-1)(x)=0

令x=0，则f⁽ⁿ⁺¹⁾(0)-n²f^(n-1)(0)=0．而f′(0)=1，f″(0)=0，所以

f⁽ⁿ⁾(0)=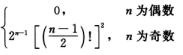

6.

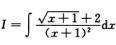
[*]+C，其中C为任意常数

解析：令t=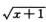，则x=t²-1，dx=2tdt．

I=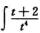·2tdt=2∫(t^-22t^-3)dt=

7.设f(x)=max{1，x²}，则∫₁^xf(t)dt=________．

[*]

解析：因为

f(x)=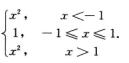

所以这是求分段函数的变限积分．

当x＜-1时，∫₁^xf(t)dt=∫₁^-1f(t)dt+∫_-1^xf(t)dt=∫₁^-11dt+∫_-1^xt²dt

=-2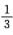t³｜_-1^x=x³-5/3．

当-1≤x≤1时，∫₁^xf(t)dt=∫₁^x1dt=x-1．

当x＞1时，∫₁^xf(t)dt=∫₁^xt²

本文档预览：3000字符，共10779字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载