考研数学二（填空题）模拟试卷200

考研数学二（填空题）模拟试卷200

填空题

1.交换二重积分∫₀¹dx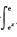

∫₁^edy∫₀^{ln y}f(x，y)dx

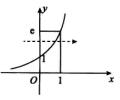
解析：根据二重积分画出来积分区域为下图，于是直接交换积分次序为

∫₁^edy∫₀^{ln y}f(x，y)dx

2.

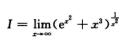
e

解析：这是∞⁰型极限，先作恒等变形

3.设f(x)连续，x→a时f(x)是x-a的n阶无穷小，则x→a时∫_a^xf(t)dt是x-a的________阶无穷小．(填阶数)

n+1

解析：

4.设f(x)=x^{sin x}(x＞0)，则f′(x)=________．

x^{sin x}[*]

解析：f(x)=x^{sin x}=e^{sin x·ln x}，f′(x)=e^{sin x·ln x}(sin x·ln x)′=x^{sin x}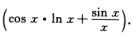

5.设(1，3)是曲线y=x³+ax²+bx+14的拐点，则a=________，b=________．

-3，-9

解析：求出y″=6x+2a．

(1，3)为该曲线拐点

y(1)=1+a+b+14=3

y″(1)=6+2a=0

a=-3，b=-9．又

y″(x)=6x-6=6(x-1)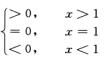

6.

[*]

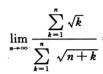
解析：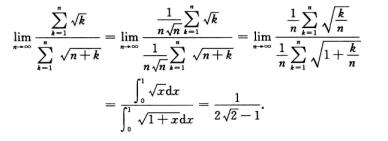

7.I=∫₁^+∞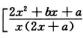

2(e-1)，2(e-1)

解析：I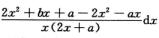=∫₁^+∞=∫₁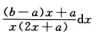^+∞积分I收敛，则b=a(否则I发散)．

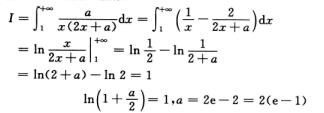
8.微分方程yy″+2(y′)²=0满足初始条件y(0)=1，y′(0)=-1的特解是________．

[*]

解析：这是可降阶的二阶的方程(方程不显含x)．作变换p=y′=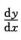，并以y为自变量，即令y′=p(y)，则y″=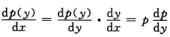，代入方程得

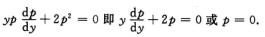
由于p=0即y′=0不符合题目要求，故只考虑方程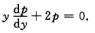

分离变量得=0，积分得ln｜p｜+2ln｜y｜=ln｜C₁｜即p=

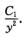
由x=0时y=1，p=y′=-1可确定常数C₁=-1．于是y′=p-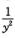，即y²dy+dx=0，积分得y³+3x=C本文档预览：3000字符，共9269字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载