
考研数学二(选择题)模拟试卷216
选择题
1.设函数z=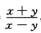 ,则dz=
,则dz=
 (A)
(A)
A.
B.
C.
D.
解析: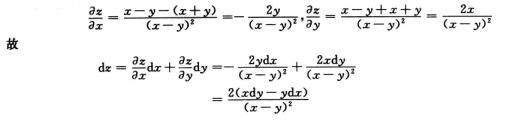
2.f(x)=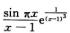 (D)
(D)
A. 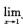 B.
B. 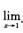 C.
C. 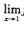 D.
D. 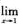 f(x)不存在,且
f(x)不存在,且 解析:
解析: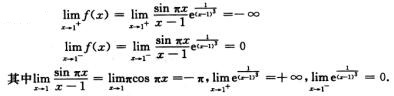
3.设f(x)在[a,+∞)连续,则“存在xn∈[a,+∞),有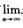 xn=+∞且
xn=+∞且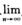 (C)
(C)
A. 充分非必要条件.
B. 必要非充分条件.
C. 充要条件.
D. 既非充分又非必要条件.
解析:
4.设f(x)=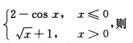 (C)
(C)
A. x=0是f(x)的极值点,但(0,1)不是曲线y=f(x)的拐点.
B. x=0不是f(x)的极值点,但(0,1)是曲线y=f(x)的拐点.
C. x=0是f(x)的极值点,且(0,1)是曲线y=f(x)的拐点.
D. x=0不是f(x)的极值点,(0,1)也不是曲线y=f(x)的拐点.
解析:显然f(x)在(-∞,+∞)连续.只须考察f(x)在x=0某空心邻域如x∈(-π/2,π/2),x≠0时f′(x)与f″(x)的变化.
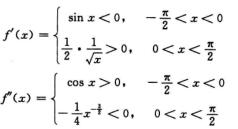
5.设f(x)=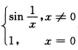 (B)
(B)
A. 在(-1,1)为无界函数.
B. 在(-1,1)为连续有界函数.
C. 在(-1,1)有间断点x=0.
D. 在[-1,1]不可积.
解析:f(x)在[-1,1]有界,只有一个间断点x=0 f(x)在[-1,1]可积
f(x)在[-1,1]可积
6.设F(x)=∫0x(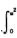 (B)
(B)
A. 在(-∞,0)是凹的,在(0,+∞)是凸的.
B. 在(-∞,0)是凸的,在(0,+∞)是凹的.
C. 在(-∞,+∞)是凹的.
D. 在(-∞,+∞)是凸的.
解析:
7.设f(x)在[0,1]上连续,在(0,1)可导且f′(x)<0(x∈(0,1)),则(A)
A. 当0<x<1时∫0xf(x)dt>∫01xf(t)dt.
B. 当0<x<1时∫0xf(x)dt=∫01xf(t)dt.
C. 当0<x<1时∫0xf(x)dt<∫01xf(t)dt.
D. 以上结论均不正确.
解析:
8.设函数f(x)连续,且满足f(x)=cos 2x-4∫0x(x-t)f(t)dt,则f(x)=(A)
A. cos 2x-xsin 2x.
B. cos 2x+xsin 2x.
C. sin 2x-xcos 2x.
D. sin 2x+xcos 2x.
解析:在题设的积分等式中令x=0可得f(0)=1.又题设积分等式可改写成
f(x)=cos 2x-4x∫0xf(t)dt+4∫