考研数学二（选择题）模拟试卷218

考研数学二（选择题）模拟试卷218

选择题

1.(C)

A. 1/2．

B. 1/3．

C. 2/3．

D. 3/4．

解析：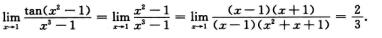

2.若(D)

A. k=2，a=1．

B. k=-2，a=-1．

C. k=2，a=-2．

D. k=2，a=-1．

解析：

3.设f(x)=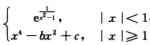(A)

A. (2，1)．

B. (1，0)．

C. (1/2，-1/2)．

D. (3，2)．

解析：｜x｜≠1时显然可导．由于f(x)是偶函数，故只须考察x=1．

首先要求f(x)在x=1连续，即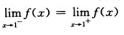=f(1)，也即

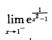=1-b+c，0=1-b+c

又f′₊(1)=(x⁴-bx²+c)′｜_x=1=4-2b．

4.设f(x)在[a，b]可导，f(a)=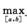(D)

A. f′₊(a)=0．

B. f′₊(a)≥0．

C. f′₊(a)＜0．

D. f′₊(a)≤0．

解析：考察f′₊(a)．

f′₊(a)=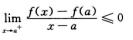

5.考察下列叙述：

①设f²(x)在x=x₀连续，则f(x)在x=x₀连续．

②设f(x)在x=x₀连续，则｜f(x)｜在x=x₀连续．

③设｜f(x)｜在[a，b]可积，则f(x)在[a，b]可积．

④设f(x)在[a，b]有界，只有有限个间断点，则｜f(x)｜在[a，b]可积，即在[a，b]存在定积分．

我们可知(C)

A. 只有①，②正确．

B. 只有②，③正确．

C. 只有②，④正确．

D. 只有③，④正确．

解析：

6.下列叙述错误的是(B)

A. 设f(x)在[-a，a]上连续为奇函数，则f(x)在[-a，a]上的全体原函数为偶函数．

B. 设f(x)在[-a，a]上连续为偶函数，则f(x)在[-a，a]上的全体原函数为奇函数．

C. 设f(x)在(-∞，+∞)内连续，以T为周期且为奇函数，则∫₀^xf(x)dt也是以T为周期的函数．

D. 设f(x)在(-∞，+∞)内连续，以T为周期，又∫₀^+∞f(x)dx收敛，则∫₀^xf(x)dt也是以T为周期的函数．

解析：因

∫f(x)dx=∫₀^xf(t)dt+C，C为任意常数

当f(x)为偶函数时∫₀^xf(t)dt为奇函数，仅当C=0时∫₀^xf(t)dt+C才是奇函数．

因此，f(x)为偶函数时，f(x)在[-a，a]只有唯一的一个原函数为奇函数即∫₀^xf(t)dt．B是错误的，选B．

7.已知y₁(x)和y₂(x)是方程y′+p(x)y=0的两个不同的特解，则该方程的通解为(D)

A. y=Cy₁(x)．

B. y=Cy₂(x)．

C. y=C₁y₁(x)+C₂y₂(x)．

D. y=C(y₁(x)-y₂(x))．

解析：由于y₁(x)和y₂(x)是方程y′+p(x)y=0的两个不同的特解，故y₁(x)=y₂(x)为该方程的一个非零解，则y=C(y₁(x)-y₂(x))为该方程的通解．

8.二元函数f(x，y)=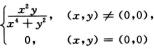(D)

A. 连续．

B.

本文档预览：3000字符，共12140字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载