考研数学二（选择题）模拟试卷213

考研数学二（选择题）模拟试卷213

选择题

1.设a是常数，则当函数f(x)=asin x+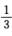(C)

A. 0．

B. 1．

C. 2．

D. 3．

解析：显然f(x)可导，则极值点必然为驻点，又有

f′(x)=acos x+cos 3x

故f′(π/3)=a/2-1=0，故a=2．

2.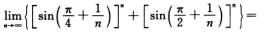(B)

A. -1．

B. 1．

C. e．

D. e^π/4．

解析：

3.设f(x)=(C)

A. x=0与x=1都是f(x)的第一类间断点．

B. x=0与x=1都是f(x)的第二类间断点．

C. x=0是f(x)的第一类间断点，x=1是f(x)的第二类间断点．

D. x=0是f(x)的第二类间断点，x=1是f(x)的第一类间断点．

解析：

4.设f(x)在x₀可导，且f′(x₀)＞0，则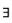(C)

A. f(x)在(x₀-δ，x₀+δ)单调上升．

B. f(x)＞f(x₀)，x∈(x₀-δ，x₀+δ)，x≠x₀．

C. f(x)＞f(x₀)，x∈(x₀，x₀+δ)．

D. f(x)＜f(x₀)，x∈(x₀，x₀+δ)．

解析：由条件出发，按导数定义

f′(x₀)=

及极限的不等式性质可知，存在δ＞0，当x∈(x₀-δ，x₀+δ)，x≠x₀时，

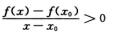
5.曲线y=(D)

A. 既有铅直又有水平与斜渐近线．

B. 仅有铅直渐近线．

C. 只有铅直与水平渐近线．

D. 只有铅直与斜渐近线．

解析：

6.设n，m为正整数，I_n，m=∫₀¹xⁿln^mxdx是(B)

A. 定积分且值为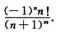B. 定积分且值为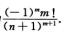C. 反常积分且发散．

D. 反常积分且值为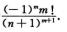解析：被积函数f(x)=xⁿln^mx虽在x=0无定义，但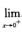xⁿln^mx=0，若补充定义f′(0)=0，则f(x)在[0，1]上连续，因而∫₀¹xⁿln^mxdx是定积分．

I_n，m=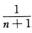∫₀¹ln^mxdxⁿ⁺¹=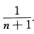xⁿ⁺¹ln^mx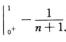∫₀¹xⁿ⁺¹mln^m-1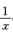x·dx

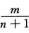=-∫₀¹xⁿln^m-1xdx=-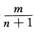I_{n，m-1本文档预览：3000字符，共11192字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载}