
考研数学二(选择题)模拟试卷222
选择题
1.∫15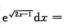 (B)
(B)
A. e3.
B. 2e3.
C. 3e3.
D. 4e4.
解析:令t=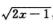 ,则∫15
,则∫15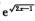
2.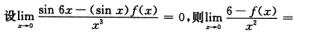 (B)
(B)
A. 0.
B. 35.
C. 36.
D. ∞.
解析: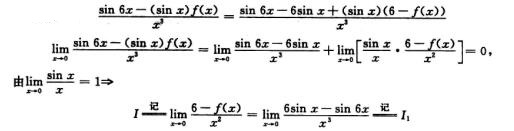
用泰勒公式
sin x=x-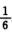 x3+o(x3),6sin x=6x-x3+o(x3)
x3+o(x3),6sin x=6x-x3+o(x3)
sin 6x=6x-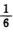 (6x)3+o(x3),-sin 6x=-6x+36x3+o(x3)
(6x)3+o(x3),-sin 6x=-6x+36x3+o(x3)
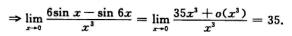
3.设函数g(x)在x=a点处连续,f(x)=|x-a|g(x)在x=a点处可导,则g(a)满足(C)
A. g(a)=a.
B. g(a)≠a.
C. g(a)=0.
D. g(a)≠0.
解析:因为f(x)=|x-a|g(x)在x=a点处可导,所以
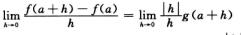
存在.而函数g(x)在x=a点处连续,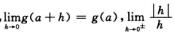
4.以下四个命题中,正确的是(C)
A. 若f′(x)在(a,b)内连续,则f(x)在(a,b)内有界.
B. 若f′(x)在(a,b)内连续,则f(x)在(a,b)内有界.
C. 若f′(x)在(a,b)内有界,则f(x)在(a,b)内有界.
D. 若f′(x)在(a,b)内有界,则f(x)在(a,b)内有界.
解析:联系f′(x)与f(x)的是拉格朗日中值定理.取定x0∈(a,b),则由拉格朗日中值定理知,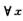
5.下述结论不正确的是(C)
A. ∫0π/4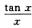 B. ∫02πcos x·ln(2+cos x)dx>0.
B. ∫02πcos x·ln(2+cos x)dx>0.
C. ∫02π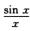 D. ∫0π/2
D. ∫0π/2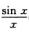 解析:下面来证明C不正确.
解析:下面来证明C不正确.
∫02π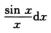 =∫0π
=∫0π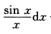 +∫π2π
+∫π2π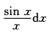
对于第2个积分,作变量变换,命x=π+t,当x=π时t=0;x=2π时t=π,于是

6.设f(x)=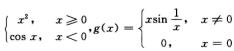 (D)
(D)
A. f(x)与g(x)都存在原函数.
B. f(x)与g(x)都不存在原函数.
C. f(x)存在原函数,g(x)不存在原函数.
D. f(x)不存在原函数,g(x)存在原函数.
解析:这是讨论原函数的存在性问题.我们知道,若F(x)在(a,b)连续,则F(x)在(a,b)一定存在原函数,这里g(x)在(-1,1)连续,所以g(x)在(-1,1)存在原函数.
余下的是f(x)在(-1,1)是否存在原函数(x=0是
本文档预览:3000字符,共14897字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载