考研数学二（选择题）模拟试卷215

考研数学二（选择题）模拟试卷215

选择题

1.∫₁^eln xdx=(C)

A. e．

B. 0．

C. 1．

D. e+1．

解析：∫₁^eln xdx=xln x｜₁^e-∫₁^e1dx=e-e+1=1．

2.设u_n=(1+1/2)(1+1/2²)…(1+1/2ⁿ)，则下列命题正确的是(B)

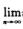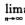A. B. C. D. 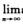u_n不存在，且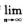解析：u_n+1=u_n(1+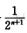)＞u_n，所以{u_n}为单调增数列．

记f(x)=e^x-1-x，则f′(x)=e^x-1＞0(x＞0)，而f(0)=0，所以f(x)＞0(x＞0)．

u_n=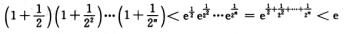

3.“f(x)在x₀点连续”是｜f(x)｜在x₀点连续的(A)

A. 充分条件，但不是必要条件．

B. 必要条件，但不是充分条件．

C. 充分必要条件．

D. 既不是充分，也不是必要条件．

解析：

4.设f(x)具有二阶连续导数，且f(1)=0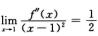，(B)

A. f(1)是f(x)的极大值．

B. f(1)是f(x)的极小值．

C. (1，f(1))是曲线f(x)的拐点坐标．

D. f(1)不是f(x)的极值，(1，f(1))也不是曲线f(x)的拐点坐标．

解析：特殊选取f(x)满足：f′(x)=1/2(x-1)²．

取f(x)=1/24(x-1)⁴，则f(x)满足题中条件，f(x)在x=1处取极小值，而其余均不正确．因此选B。

5.设F(x)是f(x)在(a，b)上的一个原函数，则f(x)+F(x)在(a，b)内(C)

A. 可导．

B. 连续．

C. 存在原函数．

D. 是初等函数．

解析：因F(x)是f(x)在(a，b)上的一个原函数，所以F′(x)=f(x)，因此F(x)在(a，b)上连续，于是F(x)在(a，b)上存在原函数，从而f(x)+F(x)在(a，b)上存在原函数．因此选C．

6.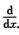(A)

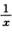A. B. 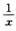C. ln(1+ln x)-ln(1+2x)．

D. ln(1+ln x)-2ln(1+2x)．

解析：

7.设f(x)为连续函数，∫₁²f(x)dx=1，F(t)=∫₁^t[f(y)∫_y^tf(x)dx]，则F′(2)=(B)

A. 2f(2)．

B. f(2)．

C. -f(2)．

D. 0．

解析：变限积分函数F(t)=∫₁^t[f(y)∫_y^tf(x)dx]dy，y是积分变量，被积函数f(y)∫_y^tf(x)dx又含变限积分函∫_y^tf(x)dx，作为y的函数

(∫_y^tf(x)dx)′=-f(y)

于是

F(t)=∫₁^t[f(y)∫_y^tf(x)dx]dy=-∫₁^t(∫_y^tf(x)dx)d(∫_y^tf(x)dx)

=-1/2(∫_y^tf(x)dx)²｜_y=1^y=t=1/2(∫₁^tf(x)dx)²

F′(t)=f(x)∫₁^{t本文档预览：3000字符，共13102字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载}