
考研数学二(填空题)模拟试卷201
填空题
1.不定积分∫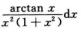
[*]
解析:
2.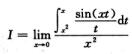
1
解析:
3.已知当x→0时F(x)=∫0x-sin xln(1+t)dt是xn的同阶无穷小,则n=________.
6
解析:确定n>0使得
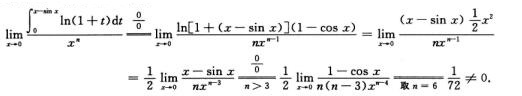
其中
ln[1+(x-sin x)]~x-sin x (x→0)
1-cos x~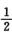
4.f(x)=x2(x+1)2(x+2)2(x+3)2,则f″(0)=________.
72
解析:记g(x)=(x+1)2(x+2)2(x+3)2,则f(x)=x2g(x),f′(x)=2xg(x)+x2g′(x),f″(x)=2g(x)+4xg′(x)x2g″(x),所以f″(0)=2g(0)=72.
5.设f(x)=3x2+Ax-3(x>0),A为正常数,则A至少为________时,有f(x)≥20(x>0).
64
解析:为使f(x)≥20,只要3x5+A≥20x3即20x3-3x5≤A.设g(x)=20x3-3x5,则A至少是g(x)在(0,+∞)内的最大值.
因
g′(x)=60x2-15x4-15x3(4-x2)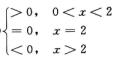
6.I1∫cos4xdx=________,I2=∫sin4xdx=________.
[*]+C2,其中C1,C2为任意常数.
解析:I1+I2=∫[(sin2x+cos2x)2–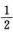 sin22x]dx
sin22x]dx
=∫[1-1/4(1-cos 4x)]dx=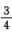 x+
x+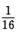 sin 4x+C3,
sin 4x+C3,
I1-I2=∫(cps4x-sin4x)dx=∫cos 2xdx=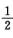 sin 2x+C4,
sin 2x+C4,
因此
I1=1/2[(I1+I2)+(I1-I2)]=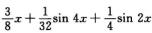 +C1,
+C1,
I2=1/2[(I1+I2)-(I1-I2)]=
7.∫0+∞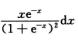
ln 2
解析:作恒等变形后,对无穷积分作分部积分.
∫0+∞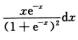 =∫0+∞
=∫0+∞本文档预览:3000字符,共13054字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载
