考研数学二（选择题）模拟试卷227

考研数学二（选择题）模拟试卷227

选择题

1.设函数f(x)=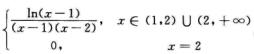(B)

A. 在(1，2)区间有界．

B. 在(2，+∞)区间有界．

C. 在(1，+∞)区间有界．

D. 在(1，2)和(2，+∞)区间都无界．

解析：

2.设f(x)=∫₀^xte^{sin t}dt，则当x→0时，f(x)为无穷小x的阶为(B)

A. 一阶．

B. 二阶．

C. 三阶．

D. 四阶．

解析：当x→0时，设f(x)为x的p阶无穷小，则

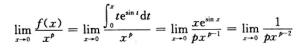
当p=2时，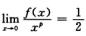

3.设常数a＞1，y=x为曲线y=a^x的切线，则(B)

A. a=e，切点为(e，e)．

B. a=e^1/e切点为(e，e)．

C. a=e，切点为(e^1/e，e^1/e)．

D. a=e^1/e，切点为(e^1/e，e^1/e)．

解析：设切点为(x₀，y₀)，则因为y=x为曲线y=a^x的切线，

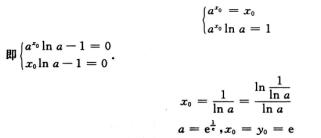
4.函数f(x)=3arccos x-arccos(3x-4x³)在[-1/2，1/2](C)

A. 单调上升．

B. 单调下降．

C. 为常数．

D. 有两个单调区间．

解析：归结为求f′(x)．

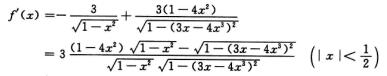
考察f′(x)的分子：

[(1-4x²)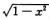]²=(1-8x²+16x⁴)(1-x²)=1-9x²+24x⁴-16x⁶

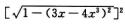
5.I=∫₀¹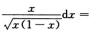(B)

A. π．

B. π/2．

C. π/4．

D. π/8．

解析：令x=sin²t，则

I=∫₀^π/2

6.设有下列命题

①设f(x)在(-∞，+∞)内连续是奇函数，则∫_-∞^+∞f(x)dx=0．

②设f(x)在(-∞，+∞)内连续，又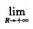(A)

A. 1．

B. 2．

C. 3．

D. 4．

解析：我们要逐一分析各命题是否正确．

命题①是错的．因为

f(x)在(-∞，+∞)连续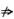∫_-∞^+∞f(x)dx收敛，如∫_-∞^+∞sin xdx发散．

命题②也是错的．如∫_-∞^+∞sin xdx发散，但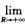∫_-R^Rsin xdx=0．

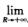∫_-R^Rf(x)dx存在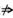

7.若A，B为非零常数，k为常数，则微分方程y″+k²y=cos x的特解可能具有形式(C)

A. Asin x+Bcos x．

B. Axcox x．

C. Axsin x．

D. Axsinx+Bxcos x．

解析：如果k≠1，对于A选项，该非齐次方程的特解形式为Asin x+Bcos x，代入方程易得特解为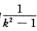cos x，即A=

本文档预览：3000字符，共11317字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载