考研数学二（选择题）模拟试卷220

考研数学二（选择题）模拟试卷220

选择题

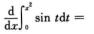1.(C)

A. sin x．

B. sin x²．

C. 2xsin x²．

D. 2xcos x²．

解析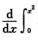：sin tdt=sin x²·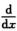

2.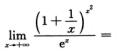(D)

A. 1．

B. e^-1/4．

C. e^-1/3．

D. e^-1/2．

解析：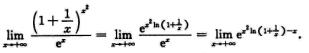

而由泰勒展开，x²ln(1+1/x)-x=x²(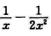+o(x^-2))-x=-1/2+o(1)，x→+∞，所以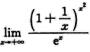

3.设f(0)=0，则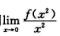(B)

A. 充分非必要条件．

B. 必要非充分条件．

C. 充分必要条件．

D. 既非充分又非必要条件．

解析：当f(0)=0时，

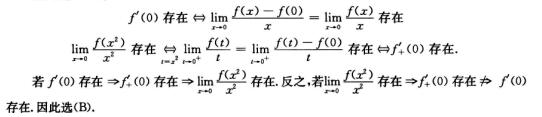
4.设f(x)=ax³-6ax²+b在区间[-1，2]上的最大值是3，最小值是-29，且a＞0，则(C)

A. a=2，b=-29．

B. a=3，b=2．

C. a=2，b=3．

D. 以上都不对．

解析：令f′(x)=3ax²-12ax=3ax(x-4)=0得x₁=0，x₂=4(不合题意舍去)

f(0)=b，f(-1)=-7a+b，f(2)=-16a+b，由于a＞0，所以，f(0)是最大值，f(2)是最小值．

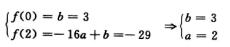
5.下列命题中有一个正确的是

B

解析：A，C，D是错的．

关于A，f(x)≥0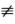，0(不恒等于0)(x∈[a，b])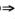∫_a^bf(x)dx≥0∫_a^bf(x)dx＞0．例如

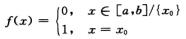
其中x₀∈[a，b]，f(x)≥0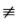，0(x∈[a，b])，∫_a^bf(x)dx=0．因此A是错的．

关于C，f(x)=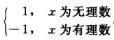，f²(x)=1，∫_a^bf²(x)dx存在，但∫_a^bf(x)dx不存在．因此C是错的．

关于D，在D的条件下，F(x)在[a，b]处处连续，x≠x₀时可导．F(x)在x=x₀处是否可导与在x=x₀处的间断点类型有关．若x=x₀是f(x)的可去间断点，则F(x)在x=x₀处可导．因为

F′(x₀)=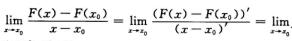

6.函数F(x)=∫_x^x+πln(1+cos²t)cos 2tdt．(A)

A. 为正数．

B. 为负数．

C. 恒为零．

D. 不是常数．

解析：因被积函数是以π为周期的函数，它在每个周期上的积分值相等，因此，

F(x)=F(0)=∫₀^πln(+cos²t)cos 2tdt=1/2∫₀^πln(+cos²t)dsin 2t本文档预览：3000字符，共11761字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载