考研数学二（填空题）模拟试卷199

考研数学二（填空题）模拟试卷199

填空题

1.y=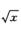

y=x/4+1

解析：y=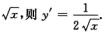

2.

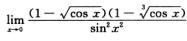
1/24

解析：洛必达法则

3.

1

解析：分子有理化，

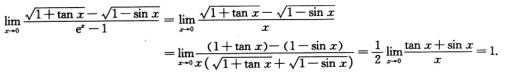
4.设f(x)在x=a处二阶导数存在，则I=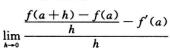

[*]

解析：用泰勒公式．

f(a+h)=f(a)+f′(a)h+f′(a)h²+o(h²) (h→0)

代入得

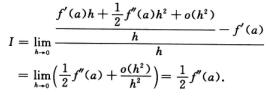
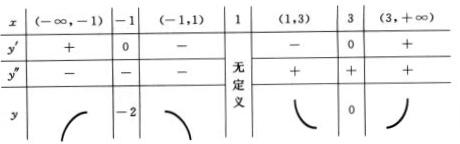
5.函数y=

(-∞，-1]，[3，+∞)；[-1，1)，(1，3]；f(-1)=-2是极大值，f(3)=0是极小值；(1，+∞)；(-∞，1)

解析：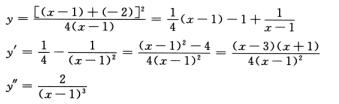

y′=0x=3，x=-1，y″≠0，x=1处y无定义．现用x=-1，x=1，x=3将定义域分成如下区间并列表：

6.设f(x)=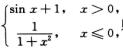

F(x)=[*]其中C为任意常数

解析：记f(x)的原函数为F(x)，则

当x＞0时，F(x)=∫(sin x+1)dx=-cos x+x+C₂；

当x≤0时，F(x)=∫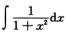=arctan x+C₁．

因为F(x)为f(x)的原函数，所以F(x)在x=0点连续，即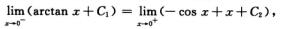

C₁=C₂=1．故f(x)的所有原函数为F(x)=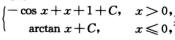

7.∫₁^+∞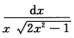

π/4

解析：

8.微分方程(xtan y+sin 2y)

[*]

解析：把x看作y的函数，则方程改写为

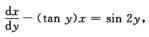
这是一阶线性方程．两边同乘得

(xcos y)=sin 2ycos y．

积分得

xcos y=0+∫₀^ysin 2tcos tdt=2∫₀^ysin tcos²tdt=-本文档预览：3000字符，共10550字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载