考研数学二（选择题）模拟试卷226

考研数学二（选择题）模拟试卷226

选择题

1.有以下命题：设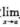f(x)=A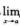，g(x)不存在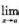，h(x)不存在，

①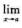(f(x)·g(x))不存在． ②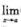(g(x)+h(x))不存在．

③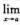(h(x)·g(x))不存在． ④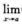(B)

A. 0．

B. 1．

C. 2．

D. 3．

解析：

2.设x→a时f(x)与g(x)分别是x-a的n阶与m阶无穷小，则下列命题中，正确的个数是

①f(x)g(x)是x-a的n+m阶无穷小．

②若n＞m，则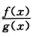(C)

A. 1．

B. 2．

C. 3．

D. 4．

解析：此类问题要逐一分析，按无穷小阶的定义：

因此①②正确．再考察

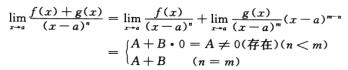
由此得，当n＜m时f(x)+g(x)是x-a的n阶无穷小．

当n=m时f(x)+g(x)是x-a的n阶(A+B≠0)或高于n阶(A+B=0)的无穷小．例如，x→0时，sin x与-x均是x的一阶无穷小，但

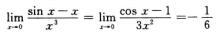
即sin x+(-x)是x的三阶无穷小；因此③不正确．

最后考察

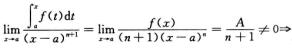
3.设f(x)为连续函数，g(x)=∫_-x⁰tf(x+t)dt，则g′(x)=(A)

A. -∫₀^xf(u)du．

B. ∫₀^xf(u)du．

C. -∫₀^-xf(u)du．

D. ∫₀^-xf(u)du．

解析：作变量代换u=x+t，则

g(x)=∫_-x⁰tf(x+t)dt=∫₀^x(u-x)f(u)du=∫₀^xuf(u)du-x∫₀^xf(u)du

g′(x)=xf(x)-∫₀^xf(u)du-xf(x)=-∫₀^xf(u)du

4.设曲线y=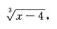(B)

A. 曲线的凸区间为(-∞，4)，凹区间为(4，+∞)，拐点为(4，0)．

B. 曲线的凹区间为(-∞，4)，凸区间为(4，+∞)，拐点为(4，0)．

C. 曲线的凸区间为(-∞，4)，凹区间为(4，+∞)，无拐点．

D. 曲线的凹区间为(-∞，4)，凸区间为(4，+∞)，无拐点．

解析：y′=1/3(x-4)^-2/3，y″=-2/9(x-4)^-5/3所以当y∈(-∞，4)时，y″＞0，曲线凹；当y∈(4，+∞)时，y″＜0，曲线凸．(4，0)为拐点．

5.I=∫₀^πx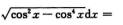(B)

A. π．

B. π/2．

C. π/3．

D. π/4．

解析：I=∫₀^πx｜cos x｜sin xdx=∫₀^π/2xcos xsin xdx-∫_π/2^πxcos xsin xdx

=-1/4∫₀^π/2xdcos 2x+1/4∫_π/2^πxdcos 2x

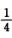=-xcos 2x｜₀^π/2+1/4∫₀^π/2cos 2xdx+本文档预览：3000字符，共12190字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载