考研数学二（选择题）模拟试卷224

考研数学二（选择题）模拟试卷224

选择题

1.设有下列命题

①数列{x_n}收敛(即存在极限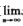x_n)，则x_n有界．

②数列极限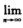x_n=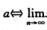x_n+l=a．其中l为某个确定的正整数．

③数列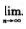x_n=x_2n-1=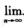x_2n=a．

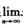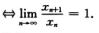④数列极限x_n存在(C)

A. 1．

B. 2．

C. 3．

D. 4．

解析：若极限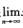x_n存在，则x_n有界．这是我们应熟悉的基本定理，即①正确．关于②，③的正确性，从直观上理解即可．

x_n：x₁，x₂，x₃，…，x_n，…

x_n+l：x_1+l，x_2+l，x_3+l，…，x_n+l，…

{x_n}中去掉前l项即{x_n+l}．

x_2n-1：x₁，x₃，x₅，…，x_2n-1，…

x_2n:x₂，x₄，x₆，…，x_2n，…

它们一起涵盖了x_n的所有项．

命题④是错的．例如x_n=n，但

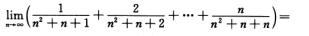2.(D)

A. 3．

B. 2．

C. 2/3．

D. 1/2．

解析：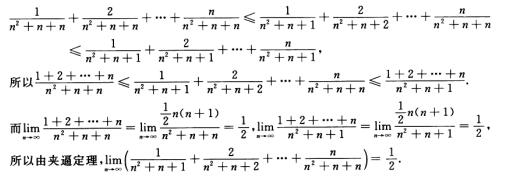

3.设f(x)在点x=a处可导，则函数｜f(x)｜在点x=a处不可导的充分必要条件是(B)

A. f(a)=0，且f′(a)=0．

B. f(a)=0，且f′(a)≠0．

C. f(a)＞0，且f′(a)＞0．

D. f(a)＜0，且f′(a)＜0．

解析：当f(a)≠0时(不论f′(a)是正值还是负值)，由连续性，在x=a附近或｜f(x)｜=f(x)，或｜f(x)｜=-f(x)，于是｜f(x)｜与f(x)在x=a有相同的可导性．由f′(a)存在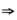｜f(x)｜′｜_x=a存在，CD被排除．

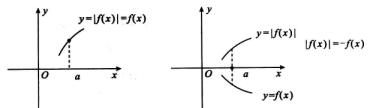
当f(a)=0，f′(a)=0时曲线y=f(x)在(a，0)点与x轴相切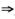y=｜f(x)｜同样在(a，0)点与x轴相切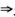｜f(x)｜′｜_x=a存在(且为零值)．A被排除．

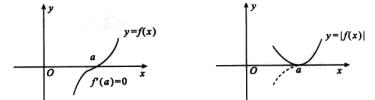
4.函数y=f(x)在(-∞，+∞)内连续，其二阶导函数的图形如图所示，则y=f(x)的拐点的个数是

(C)

A. 1．

B. 2．

C. 3．

D. 4．

解析：只须考察f″(x)=0的点与f″(x)不存在的点．

f″(x₁)=f″(x₄)=0，在x=x₁，x₄两侧f″(x)变号，故凹凸性相反，本文档预览：3000字符，共12115字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载