考研数学二（填空题）模拟试卷205

考研数学二（填空题）模拟试卷205

填空题

1.设函数f(x)为定义在(-∞，+∞)的奇函数，且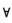

0

解析：由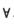x∈(-∞，+∞)，f(x+2)-f(x)=f(2)可知，f(x)是以2为周期的周期函数的充分必要条件为f(2)=0．

因为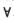

2.设x₀=0，x_n=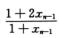(n=1，2，3，…)，则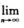

[*]

解析：显然

0＜x_n= (n=1，2，3，…)

即x_n有界．

令f(x)=2-x_n+1=f(x_n)(n=1，2，3，…)单调．

因此x_n收敛，记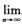x_n=a．

对递归方程x_n=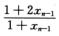两边取极限得a=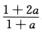，即

a²-a-1=0

解得a=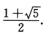

3.设f(x)=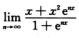

(-∞，+∞)

解析：先求出f(x)．

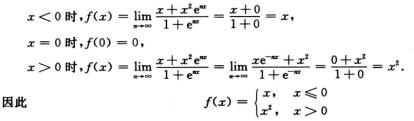
4.设f(x)=∫₀^xln(1+sin t)dt，则f′(x)=________．

[*]

解析：f′(x)=ln(1+sin x)

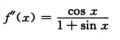
5.设函数f(x)在x=0处连续，且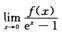

y=-[*]x

解析：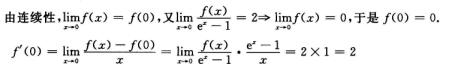

曲线y=f(x)在x=0处的法线斜率为-1/2，法线方程为y=-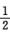

6.设f(x)为连续函数，φ为常数，∫₀^2πf(sin(x+φ))dx=A∫_-π/2^π/2f(sin x)dx，则A=________．

2

解析：按题意的提示，我们应把左端定积分变形并作变量替换得

I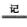∫₀^2πf(sin(x+φ))dx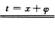∫_φ^2π+φf(sin t)dt

被积函数以2π为周期，由周期函数的积分性质

I=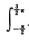f(sin t)dt=∫_-π/2^π/2f(sin t)dt+

7.I=∫_-π/2^π/2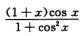

[*]

解析：I

本文档预览：3000字符，共10050字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载