考研数学二（选择题）模拟试卷221

考研数学二（选择题）模拟试卷221

选择题

1.已知函数f(x)的一个原函数ln²x，则∫xf′(x)dx=(D)

A. ln²x+C．

B. -ln²x+C．

C. ln x-ln²x+C．

D. 2ln x-ln²x+C．

解析：由已知∫f(x)dx=ln²x+C，f(x)=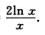

2.已知I=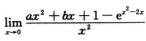(A)

A. a=5，b=-2．

B. a=-2，b=5．

C. a=2，b=0．

D. a=3，b=-3．

解析：将已知条件改写成

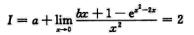
即 I₂=2-a

其中I₁=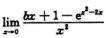存在，由此定出参数a与b．

用泰勒公式：

由极限与无穷小的关系

I₁=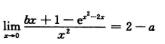

可写成

bx+1-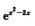=(2-a)x²+o(x²)

由泰勒公式

e^t=1+t+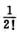t²+o(t²)(t→0)

令t=x²-2x，则

t²=(x²-2x)²=x⁴-4x³+4x²=4x²+o(x²)(x→0)

o(t²)=o(x²) (x→0)

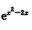=1+(-2x+x²)+1/2(4x²)+o(x²)

=1-2x+3x²+o(x²)

于是 bx+1-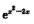

3.设f(x)是以3为周期的可导函数且f′(4)=1，则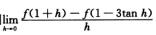(C)

A. 5．

B. 3．

C. 4．

D. 7．

解析：f′(x)也以3为周期辛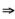f′(1)=f′(4)，我们可由f′(1)求得极限值I．

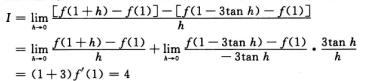
4.设f(x)在[a，b]上连续，在(a，b)内存在二阶导数且f(a)＜0，f(b)＞0，f′(x)＞0．则f(x)在(a，b)内(B)

A. 没有零点．

B. 正好有1个零点．

C. 正好有2个零点．

D. 有多于2个零点．

解析：由f(a)＜0，f(b)＞0知，f(x)在(a，b)上至少有1个零点．不选A．下面证正好1个零点．

用反证法，设至少有2个零点：x₁＜x₂．在区间[a，x₁]与[x₁，x₂]上用拉格朗日中值定理

f(x₁)-f(a)=f′(ξ₁)(x₁-a)

有

f(ξ₁)＞0，(a＜ξ₁＜x₁)

f(x₂)-f(x₁)=f′(ξ₂)(x₂-x₁)

有

f′(ξ₂)=0，(x₁＜ξ₂＜x₂)

推得f′(ξ₂)＜f′(ξ₁)，(ξ₁＜ξ₂)．再在[ξ₁，ξ₂]上用拉格朗日中值定理，有

f′(ξ₂)-f′(ξ₁)=f″(ξ₃)(ξ₂-ξ₁)＞0

矛盾．

5.设f(x)在[a，b]连续，则下列结论中正确的个数为

①f(x)在[a，b]的任意子区间[α，

本文档预览：3000字符，共13133字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载