考研数学二（填空题）模拟试卷203

考研数学二（填空题）模拟试卷203

填空题

1.已知f(2)=2，∫₀²f(x)dx=4，∫₀²xf′(x)dx=________．

0

解析：∫₀²xf′(x)dx=∫₀²xdf(x)=xf(x)｜₀²-∫₀²f(x)dx=4-4=0．

2.设a＞0，则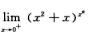

1

解析：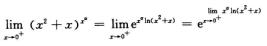

3.设f(x)=

-1

解析：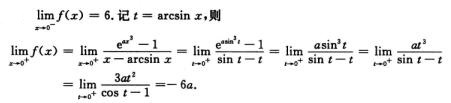

4.设y=y(x)由方程y=sin(x+y)确定，则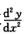

[*]

解析：将方程两边对x求导得

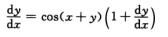
解出

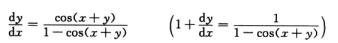
再对x求导得

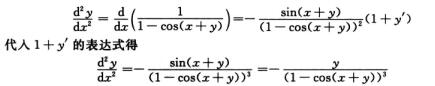
5.设有界函数f(x)在(c，+∞)内可导，且

0

解析：因f(x)在(c，+∞)可导，有界．

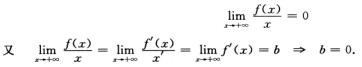
6.I=∫₀¹arcsin x·arccos xdx=________．

-π/2+2

解析：令t=arcsin x，则x=sin t，dx=cos tdt，arccos x=π/2-t，

I=∫₀^π/2(π/2-t)cos tdt=∫₀^π/2t(π/2-t)d(sin t)

=t(π/2-t)(sin t)｜₀^π/2-∫₀^π/2(π/2-2t)sin tdt

=∫₀^π/2(π/2-2t)d(cos t)=(π/2-2t)cos t｜₀^π/2+2∫₀^π/2cos tdt=-π/2+2．

7.若不定积分∫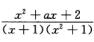

-1

解析：用待定系数法将被积函数分解

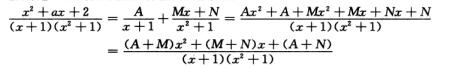
8.设y=y(x)是二阶常系数线性微分方程y″+2my′+n²y=0满足y(0)=a与y′(0)=b的特解，其中m＞n＞0，则∫₀^+∞y(x)dx=________．

[*]

解析：y″+2my′n²y=0的特征方程λ²+2mλ+n²=0的特征根是

λ₁=-m+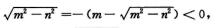

λ₂=-m-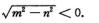

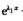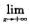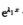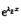由此可见微分方程的任何一个解y=C₁+C₂都满足y=0．又因y′=C₁λ₁+C₂λ₂，从而又有本文档预览：3000字符，共9885字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载