考研数学二（填空题）模拟试卷198

考研数学二（填空题）模拟试卷198

填空题

1.如果函数f(x)=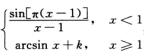

π/2

解析：显然f(x)在(-∞，1)和(1，+∞)上均连续，下面讨论x=1处的连续性．

f(1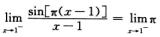^–=·cos[π(x-1)]=π

f(1⁺)=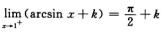

2.

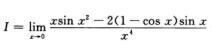
0

解析：这是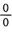型极限，先作如下变形：

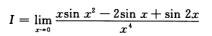
可用的方法是洛必达法则(计算较繁)与泰勒公式．

注意泰勒公式

sin x=x-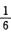x³+o(x⁴) (x→0) (x⁴项系数为0)

xsin x²=x(x²+o(x⁴))=x³+o(x⁴)

-2sin x=-2(x-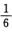x³+o(x⁴))=-2x+x³+o(x⁴)

sin 2x=2x-(2x)³+o(x⁴)=2x-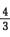x³+o(x⁴)

相加得

xsin x²-2sin x+sin 2x=0+o(x⁴) (x→0)

因此

3.设a，b，p为非零常数，则I=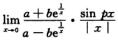

-p

解析：因为｜x｜是分段函数，分界点是x=0，又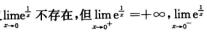=0，所以要分别求左、右极限．

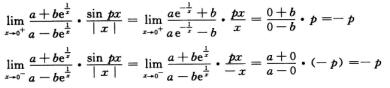
4.设f(x)在x=0可导且f(0)=1，f′(0)=3，则I=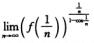

e⁶

解析：这是指数型的数列极限，先化为

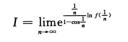
转化为求

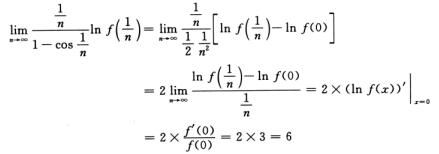
5.设y=y(x)是由方程2y³-2y²+2xy-x²-1确定的，则y=y(x)的极值点是________．

x=1

解析：将方程2y³-2y²+2xy-x²=1两边对x求导，得

6y²y′-4yy′+2y+2xy′-2x=0

整理得 y′(3y²-2y+x)=x-y (1)

令y′=0，有x=y，将其代入2y³-2y²+2xy-x²=1得

2x³-x²-1=(x³-1)+(x³-x²)=0，即(x-1)(2x²+x+1)=0，于是x=1是唯一的驻点．此时，y=x=1．

进一步判断x=1是否是极值点：

对(1)求导 y″(3y²-2y+x)+y′(3y²-2y+x)′_x=1-y′

把x=1，y=1，y′(1)=0代入上式，得y″(1)=1/2＞0，于是y(x)只有极值点为x=1，它是极小值点．

本文档预览：3000字符，共9936字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载