
考研数学二(选择题)模拟试卷214
选择题
1.设y=xn+ex,则y(n)=(C)
A. ex.
B. n!.
C. n!+ex.
D. n!+nex.
解析:y(n)=(xn+ex)(n)=(xn)(n)+(ex)(n),显然(xn)(n)=n!,(ex)(n)=ex.故有y(n)=(xn+ex)(n)=n!+ex.
2.当n→∞时,数列(1+1/n)n-e是1/n的(D)
A. 高阶无穷小.
B. 低阶无穷小.
C. 等价无穷小.
D. 同阶但非等价无穷小.
解析:该题就是要计算极限

直接转化为求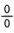 型函数极限,然后用洛必达法则.
型函数极限,然后用洛必达法则.

3.设f(x)在点x0的某邻域内有定义,且f(x)在x0间断,则在点x0处必定间断的函数是(B)
A. f(x)sin x.
B. f(x)+sin x.
C. f2(x).
D. |f(x)|.
解析:若f(x)+sin x在x=x0连续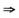
4.设f(x)对一切x∈(-∞,+∞)满足方程(x-1)f″(x)+2(x-1)[f′(x)]3=1-e1-x,且f(x)在x=a(a≠1)处f′(a)=0,则x=a(A)
A. 是f(x)的极小值点.
B. 是f(x)的极大值点.
C. 不是f(x)的极值点.
D. 是f(x)的拐点.
解析:因f′(a)=0,于是有(a-1)f″(a)=1-e1-a,显然
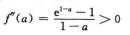
5.函数f(x)=3ln x-x(C)
A. 没有零点.
B. 有1个零点.
C. 有2个零点.
D. 有3个零点.
解析:
6.设sin xln|x|是f(x)的一个原函数,则不定积分∫xf′(x)dx=(B)
A. xcos xln|x|+x·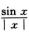 B. xcos xln|x|+sin x-sin xln|x|+C.
B. xcos xln|x|+sin x-sin xln|x|+C.
C. cos xln|x|-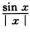 D. 以上均不正确.
D. 以上均不正确.
解析:
7.设an=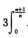 x2n-1
x2n-1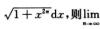 (B)
(B)
A. (1+e)3/2+1.
B. (1+e2)3/2-1.
C. (1+e-1)3/2+1.
D. (1+e)3/2-1.
解析:
8.设f(x)具有一阶连续导数,f(0)=0,du(x,y)=f(x)ydx+[sin x-f(x)]dy,则f(x)等于(B)
A. cos x+sin x-1.
B. 1/2(cos x+sin x-e-x).
C. cos x-sin x+xex.
D. cos x-sin x+xe-x.
解析:
9.设f(x,y)在点(x0,y0)处两个偏导数f′x(x0,y0),f′y(x0,y0)都存在,则(C)
A. f(x,y)在(x0,y0)处连续.
B. 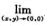 C.
C. 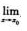 f(x,y0)=
f(x,y0)=