考研数学二（一元函数积分学的计算、一元函数积分学的应用（二）——积分等式与积分不等式）模拟试卷2

考研数学二（一元函数积分学的计算、一元函数积分学的应用（二）——积分等式与积分不等式）模拟试卷2

选择题

1.定积分∫₀¹=（ ）．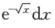

(B)

A.

B.

C.

D.

解析：令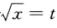，则x=t²，dx=2tdt，且当x=0时t=0；当x=1时t=1。所以

∫₀¹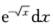=2∫₀¹te^-tdt=-2te^-t|₀¹+2∫₀¹e^-tdt

=2e^-1-2e^-t|₀¹=-4e^-1+2=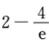

2.若e^-x是f(x)的一个原函数，则(A)

A. -1/4

B. -1

C. 1/4

D. 1

解析：由于f(x)=(e^-x)’=-e^-x，所以f(lnx)=-e^{-ln x}=-1/x，从而

3.若函数f(x)连续，g(x)=∫₀^2x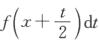，则当x→0+时，g(x)是(A)

A. 高阶无穷小

B. 低阶无穷小

C. 等价无穷小

D. 同阶非等价无穷小

解析：在g(x)=∫₀^2x，则

g(x)=∫₀^2x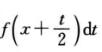=2∫_x^2xf(u)du，

这表明当x→0⁺时，g(x)是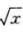

4.设f(x)在x=0的某邻域内连续，在x=0可导，且f(0)=0，ψ(x)=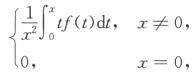(D)

A. 不连续

B. 连续但不可导

C. 可导但ψ‘(x)在x=0处不连续

D. 可导且ψ’(x)在x=0处连续

解析：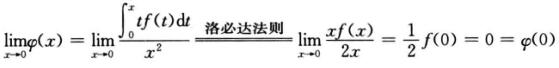

因此ψ(x)在x=0处连续．

当x≠0时，

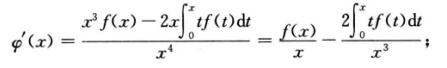
当x=0时，

5.若连续周期函数y=f(x)(不恒为常数)对任何x，恒有∫_-1^x+6f(t)dt+∫_x-3¹f(t)dt=14成立，则f(x)的周期是（ ）．(C)

A. 7

B. 8

C. 9(D)10

解析：由∫_-1^x+6f(t)dt+∫_x-3⁴ f(t)dt=14求导，得

f(x+6)-f(x-3)=0，

即f(x+6)=f(x-3)，令x-3=t，则x=t+3，代入f(x+6)=f(x-3)中得F(t+9)=f(t)，

所以f(x)以9为周期．

故正确选项为(C)．

6.设f(x)在[-a，a]上是连续的偶函数，a＞0

本文档预览：3000字符，共15134字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载